Momentum Equation

By /

In fluid mechanics, the momentum equation is a direct application of Newton’s second law of motion to a moving fluid. Just as Newton’s law states that the net force on a body equals the rate of change of its momentum, in fluid flow we relate the forces acting on a fluid region to how its momentum changes over time.

This equation forms the backbone of aerodynamic force analysis—explaining how lift, drag, and thrust arise from pressure and shear forces acting on air as it flows around objects.

1️⃣ Physical Basis: Newton’s Second Law for Fluids

Newton’s second law for a particle is:

\mathbf{F} = \frac{d\mathbf{p}}{dt}

Where:

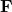  • \mathbf{F} : net external force
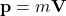  • \mathbf{p} = m\mathbf{V} : momentum of the object

In a fluid, we extend this idea to many fluid particles and express the total rate of change of momentum inside a control volume as the sum of:

  • Rate of accumulation of momentum inside the volume, and
  • Net outflow of momentum through the control surface.

The momentum equation balances these momentum changes with the net external forces acting on the control volume.

2️⃣ Integral Form of the Momentum Equation

For a fixed control volume, the integral form of the momentum equation in vector form is:

\frac{d}{dt} \int_{CV} \rho \mathbf{V} , dV + \int_{CS} \rho \mathbf{V} (\mathbf{V} \cdot d\mathbf{A}) = \sum \mathbf{F}_{\text{external}}

Where:

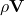  • \rho \mathbf{V} : momentum per unit volume
  • First term: rate of change of momentum inside the control volume
  • Second term: net flux of momentum across the control surface
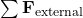  • \sum \mathbf{F}_{\text{external}} : sum of all external forces acting on the fluid

External forces may include:

  • Surface forces (pressure, viscous shear stress)
  • Body forces (gravity, electromagnetic forces)

This form is very useful in engineering applications—for example, computing thrust by applying the momentum equation to a jet engine exhaust.

3️⃣ Differential Form of the Momentum Equation (Navier–Stokes Equation)

To describe the motion of fluid at a point, we use the differential form of the momentum equation. This form is derived by applying Newton’s second law to an infinitesimal fluid element.

For a compressible, viscous fluid, the equation is:

\rho \frac{D \mathbf{V}}{D t} = -\nabla p + \mu \nabla^2 \mathbf{V} + \rho \mathbf{g}

Where:

  • \frac{D \mathbf{V}}{Dt} : material derivative of velocity (acceleration of a fluid particle)
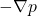  • -\nabla p : pressure force per unit volume
  • \mu \nabla^2 \mathbf{V} : viscous force (for a Newtonian fluid)
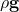  • \rho \mathbf{g} : body force due to gravity

This is known as the Navier–Stokes equation, which is the most general form of the momentum equation used in fluid dynamics.

4️⃣ Inviscid Flow Simplification (Euler Equation)

In many aerodynamic applications, especially external flows where viscosity effects are small compared to pressure forces, the fluid is assumed to be inviscid (zero viscosity).

In that case, the Navier–Stokes equation simplifies to the Euler equation:

\rho \frac{D \mathbf{V}}{D t} = -\nabla p + \rho \mathbf{g}

This form neglects viscous terms but retains pressure and body forces. It is widely used in potential flow theory and in modeling high-speed external flows away from boundary layers.

5️⃣ Steady, One-Dimensional Momentum Equation (Example)

For a steady, one-dimensional flow through a duct (e.g., wind tunnel or jet engine inlet), the momentum equation simplifies to:

\dot{m} (V_2 - V_1) = \sum F_{\text{external}}

Where:

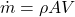  • \dot{m} = \rho A V : mass flow rate
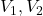  • V_1, V_2 : inlet and outlet velocities
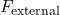  • F_{\text{external}} : net pressure force or reaction force on the control volume

This simplified form is useful for:

  • Computing thrust from jet engines
  • Determining pressure forces on objects
  • Estimating velocity changes due to pressure differences

6️⃣ Aerodynamic Applications

The momentum equation is used to explain and compute key aerodynamic phenomena:

  • Lift generation: as pressure differences across an airfoil’s surface are integrated using force balance
  • Drag and thrust: computed from changes in momentum of airflow entering and leaving control volumes
  • Boundary layer analysis: momentum loss due to friction is critical in skin-friction drag
  • Jet propulsion: thrust results from high-speed exhaust increasing momentum

In summary, the momentum equation provides a quantitative relationship between the forces acting on a fluid and the resulting motion of that fluid. It is a cornerstone of all aerodynamic force prediction and analysis.

Shopping Cart
Scroll to Top