Flow over a cylinder

By /

In potential flow theory, flow over a cylinder is modeled by combining elementary flows to satisfy the boundary conditions of an impermeable cylinder.

This topic is best understood in two main parts:

✅ Non-lifting flow over a cylinder: Uniform flow + doublet.
✅ Lifting flow over a cylinder: Uniform flow + doublet + vortex (circulation).

These models are mathematical but remain tractable, making them classic examples in theoretical aerodynamics.

1️⃣ Non-Lifting Flow Over a Cylinder

Goal: Model steady, inviscid, incompressible, irrotational flow around a stationary cylinder without circulation.

(a) Superposition Principle

We use:

  • Uniform flow: represents freestream

\phi_{uniform} = U r \cos \theta

Doublet: represents solid body blocking flow

\phi_{doublet} = -\frac{\kappa}{2\pi} \frac{\cos \theta}{r}

Combined potential:

\phi_{total} = U r \cos \theta - \frac{\kappa}{2\pi} \frac{\cos \theta}{r}

(b) Determining Doublet Strength

The cylinder boundary (radius a ) must be a streamline (no normal flow):

Stream function:

\psi_{total} = U r \sin \theta - \frac{\kappa}{2\pi} \frac{\sin \theta}{r}

On r = a:

\psi_{total} = 0 \implies U a \sin \theta - \frac{\kappa}{2\pi} \frac{\sin \theta}{a} = 0

Solving:

\kappa = 2 \pi U a^2

This ensures the streamline ψ = 0 matches the cylinder surface.

(c) Final Expressions

Velocity potential:

\phi_{total} = U \left( r + \frac{a^2}{r} \right) \cos \theta

Stream function:

\psi_{total} = U \left( r - \frac{a^2}{r} \right) \sin \theta

(d) Surface Velocity

Tangential velocity on r = a:

V_\theta = \frac{1}{r} \frac{\partial \psi}{\partial r} \Bigg|_{r=a}

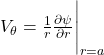
Compute:

\psi_{total} = U \left( r - \frac{a^2}{r} \right) \sin \theta

Derivative:

\frac{\partial \psi}{\partial r} = U \left( 1 + \frac{a^2}{r^2} \right) \sin \theta

At r = a:

V_\theta = \frac{1}{a} \cdot 2U \sin \theta = 2U \sin \theta

Result:

V_\theta = -2U \sin \theta

(e) Pressure Distribution

Use Bernoulli’s equation (steady, incompressible, inviscid):

\frac{p}{\rho} + \frac{V^2}{2} = \frac{p_\infty}{\rho} + \frac{U^2}{2}

At surface:

V = |V_\theta| = 2U |\sin \theta|

Coefficient of pressure:

C_p = \frac{p - p_\infty}{\frac{1}{2}\rho U^2} = 1 - \left( \frac{V}{U} \right)^2

Substitute:

C_p = 1 - 4 \sin^2 \theta

Features:

  • Minimum pressure at θ = ±90°.
  • Stagnation points at θ = 0°, 180° where V = 0.

(f) Characteristics

✅ Symmetrical flow.
✅ No net circulation.
✅ Predicts no lift.
✅ D’Alembert’s paradox: zero net drag (ideal inviscid model).

2️⃣ Lifting Flow Over a Cylinder

Goal: Model flow over a cylinder with circulation (representing lift).

(a) Adding a Vortex

Superpose a vortex of strength \Gamma :

Vortex potential:

\phi_{vortex} = -\frac{\Gamma}{2\pi} \theta

Total potential:

\phi_{total} = U \left( r + \frac{a^2}{r} \right) \cos \theta - \frac{\Gamma}{2\pi} \theta

Stream function:

\psi_{total} = U \left( r - \frac{a^2}{r} \right) \sin \theta + \frac{\Gamma}{2\pi} \ln r

(b) Effect on Streamlines

✅ Streamlines become asymmetric.
✅ Stagnation points shift off θ = 0°, 180°.
✅ Models real lifted flow (like over an airfoil cross-section).

(c) Surface Tangential Velocity

Including vortex term, the surface velocity at r = a:

V_\theta = -2U \sin \theta + \frac{\Gamma}{2\pi a}

✅ Circulation modifies the velocity distribution.
✅ Pressure difference develops between upper and lower surfaces.

(d) Pressure Coefficient with Circulation

C_p = 1 - \left( \frac{V_\theta}{U} \right)^2

Substitute Vθ:

V_\theta = -2U \sin \theta + \frac{\Gamma}{2\pi a}

Leads to:

C_p(\theta) = 1 - \left( -2 \sin \theta + \frac{\Gamma}{2\pi a U} \right)^2

Result:

  • Asymmetric pressure distribution.
  • Lower pressure on one side, higher on the other → Lift.

(e) Lift Calculation

Using the Kutta–Joukowski theorem:

L' = \rho U \Gamma

✅ Circulation directly determines lift per unit span.
✅ Increasing Γ increases lift.

(f) Interpretation

✅ Adding circulation mimics airfoil camber effects.
✅ Explains how real wings generate lift by modifying flow patterns.
✅ A key conceptual leap toward airfoil theory.

3️⃣ Summary

Non-Lifting Cylinder:

  • Uniform flow + doublet.
  • Symmetric flow.
  • No lift.

Lifting Cylinder:

  • Uniform flow + doublet + vortex.
  • Asymmetric flow.
  • Predicts lift via circulation.

In potential flow theory, these two cases demonstrate how superposition can model real aerodynamic phenomena and lay the foundation for airfoil theory and the understanding of lift generation.

Shopping Cart
Scroll to Top