Pressure, Density & Temperature Altitudes

By /

Altitude in aviation is not only a geometric height but also a way of describing atmospheric conditions that affect aircraft performance. Pressure altitude, density altitude, and temperature altitude are fundamental concepts used to interpret how the environment influences flight.

1. Pressure Altitude

1.1 Definition

  • Altitude relative to the standard atmosphere pressure levels.
  • The altitude at which the standard atmosphere has the same pressure as the current ambient pressure.
  • Determined by setting the altimeter to 29.92 inHg (1013.25 hPa).

1.2 Importance

  • Used for flight level assignments above transition altitude.
  • Standardizes vertical separation between aircraft.

1.3 Calculation

Given station pressure P:

h_p = \frac{T_0}{L} \left[ 1 - \left( \frac{P}{P_0} \right)^{\frac{LR}{g}} \right]

Where:

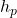  • h_p = Pressure altitude
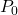  • P_0 = Sea-level standard pressure (101325 Pa)
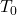  • T_0 = Sea-level standard temperature (288.15 K)
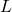  • L = Lapse rate (-0.0065 K/m)

2. Density Altitude

2.1 Definition

  • Altitude in the standard atmosphere where air density equals the actual density at the aircraft’s location.
  • Indicates performance potential under given conditions.

2.2 Concept

  • Higher density altitude means thinner air → reduced engine power, lift, and propeller efficiency.
  • Critical for takeoff and climb performance.

2.3 Calculation

First find pressure altitude h_p, then adjust for non-standard temperature T:

Approximate formula:

\text{Density Altitude} \approx h_p + 118.8 (T - T_{ISA})

Where:

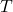  • T = Actual outside air temperature (°C)
  • T_{ISA} = ISA temperature at h_p

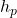
3. Temperature Altitude

3.1 Definition

  • Altitude in the standard atmosphere corresponding to a given temperature.
  • Less commonly used than pressure and density altitude.

3.2 ISA Temperature Equation

Used to relate altitude to temperature in the troposphere:

T = T_0 + L h

Rearranged for temperature altitude:

h_T = \frac{T - T_0}{L}

Where:

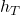  • h_T = Temperature altitude
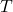  • T = Actual air temperature

4. Relationships Between Altitudes

  • Pressure altitude is the baseline, correcting for pressure deviations from standard.
  • Density altitude adjusts pressure altitude for temperature (and, less commonly, humidity).
  • High temperature or low pressure → higher density altitude → worse performance.

5. Operational Significance

5.1 Takeoff and Landing

  • Higher density altitude = longer takeoff roll, lower climb rate.
  • Critical at hot, high-elevation airports.

5.2 Aircraft Performance Charts

  • Manufacturers provide performance data corrected for density altitude.

5.3 Flight Planning

  • Pilots calculate density altitude to ensure runway length suffices for given weight and temperature.

6. Example Calculation

Given:

  • Airport elevation: 1500 ft
  • Station pressure = 28.92 inHg
  • Temperature = 30 °C

Steps:

  1. Convert station pressure to pressure altitude (using altimeter setting corrections).
  2. Find ISA temperature at pressure altitude.
  3. Compute density altitude using:

\text{Density Altitude} \approx h_p + 118.8 (T - T_{ISA})

7. Summary

Pressure altitude, density altitude, and temperature altitude translate environmental conditions into standardized reference levels. By understanding these concepts, pilots can predict aircraft performance accurately and maintain safe operations under varying atmospheric conditions.

Shopping Cart
Scroll to Top