Range and endurance are fundamental measures of airplane performance, describing how far or how long an aircraft can fly on a given amount of fuel. For propeller-driven airplanes, these quantities depend on aerodynamic efficiency, engine performance, and fuel consumption characteristics.
1. Definitions
1.1 Range
- The maximum horizontal distance an airplane can travel on a given fuel load.
- Important for planning routes, avoiding refueling stops, and optimizing mission profiles.
1.2 Endurance
- The maximum time an airplane can remain airborne on a given fuel load.
- Critical for loitering, surveillance, search and rescue, and training missions.
2. Basic Principles
The key idea: Fuel flow provides power to overcome drag.
- For propeller aircraft, fuel flow rate is proportional to power required, not thrust alone.
Power required for steady, level flight:
![]()
Where:
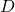 = Drag
= Drag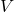 = True airspeed
= True airspeed
3. Fuel Consumption in Propeller Aircraft
3.1 Brake Specific Fuel Consumption (BSFC)
- Measure of engine efficiency.
![]()
Units: lb/(hp·hr) or kg/(kW·hr).
Lower BSFC indicates better engine efficiency.
4. Endurance for Propeller Airplane
Endurance (E) is the total time aloft:
![]()
Fuel flow rate for a piston/propeller engine is proportional to power required:
![]()
Hence:
![]()
4.1 Condition for Maximum Endurance
- Minimum power required.
At minimum power speed:
- Aircraft uses fuel most slowly per unit time.
- Best for loitering or maximizing time aloft.
Graphically:
- Power required vs. speed curve is U-shaped.
- Minimum point on the curve → maximum endurance.
5. Range for Propeller Airplane
Range (R) is the total horizontal distance flown:
![]()
Considering fuel flow rate:
![]()
But fuel flow rate is proportional to power required:
![]()
So:
![]()
5.1 Condition for Maximum Range
- Maximize the ratio
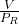 .
.
Aerodynamic Interpretation
![]()
![]()
Therefore:
![]()
Key Insight:
- Maximum range occurs at maximum lift-to-drag ratio (
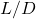 ).
).
6. Summary of Optimal Conditions
| Quantity | Optimize for |
|---|---|
| Endurance | Minimum power required |
| Range | Maximum lift-to-drag ratio |
7. Example Formulas
7.1 Endurance Estimate
If fuel flow rate ![]() :
:
![]()
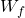 = Total fuel weight
= Total fuel weight = Fuel consumption constant
= Fuel consumption constant
7.2 Range Estimate
![]()
Maximizing ![]() yields maximum range.
yields maximum range.
8. Practical Considerations
- Altitude: Affects air density, engine efficiency, and drag.
- Weight: Heavier aircraft require more lift → higher drag.
- Propeller efficiency (
 ): Real-world propeller efficiency reduces available power for propulsion.
): Real-world propeller efficiency reduces available power for propulsion. - Wind: Tailwinds increase groundspeed (effective range), headwinds decrease it.
9. Operational Significance
- Max Endurance Flight:
- Search-and-rescue loiter
- Holding patterns before landing
- Max Range Flight:
- Ferry flights
- Long cross-country trips
Pilots consult aircraft performance charts to determine appropriate speeds for maximum range and endurance under given conditions.
10. Summary
For propeller airplanes:
- Endurance is maximized at minimum power required speed, yielding longest time aloft.
- Range is maximized at maximum
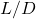 ratio speed, yielding longest distance per unit of fuel.
ratio speed, yielding longest distance per unit of fuel.
Understanding these principles enables efficient flight planning, fuel management, and mission optimization.

