Induced Drag & Zero-Lift Drag

In aerodynamics, drag is the resistive force that acts opposite to the direction of motion of an aircraft through air. It is composed primarily of two major components:

Induced Drag
Zero-lift Drag (Parasite Drag)

Understanding these components is essential for analyzing performance, optimizing aircraft design, and minimizing fuel consumption.

1. Total Drag

The total drag ( $D$ ) on an aircraft in flight is the sum of:

$D = D_i + D_0$

Where:

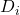$D_i$ = Induced drag
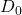$D_0$ = Zero-lift drag (or parasite drag)

2. Zero-Lift Drag (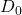 $D_0$ )

2.1 Definition

Zero-lift drag is the drag experienced by the aircraft when no lift is being produced. It is caused by:

Skin friction
Form (pressure) drag
Interference drag

It does not depend on the generation of lift, and occurs even if the aircraft is flying at zero angle of attack (e.g., in a wind tunnel test without lift).

2.2 Characteristics

Depends primarily on aircraft shape, surface area, and airspeed.
Increases rapidly with speed:

$D_0 = \frac{1}{2} \rho V^2 S C_{D0}$

Where:

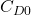$C_{D0}$ = Zero-lift drag coefficient
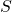$S$ = Wing reference area

3. Induced Drag (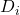 $D_i$ )

3.1 Definition

Induced drag arises as a by-product of lift generation. It is caused by:

Downwash created by the wing.
Tip vortices that tilt the lift vector rearward.

It is most significant at low speeds and high angles of attack, such as during takeoff and landing.

3.2 Derivation

Induced drag is related to lift:

$D_i = \frac{L^2}{\pi e A R \cdot \frac{1}{2} \rho V^2 S}$

Or using coefficients:

$C_{D_i} = \frac{C_L^2}{\pi e AR}$

Where:

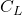$C_L$ = Lift coefficient
$e$ = Oswald efficiency factor (typically 0.7–0.9)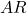
$AR$ = Aspect ratio of the wing

3.3 Characteristics

Increases with the square of lift coefficient:

$D_i \propto C_L^2$

Inversely proportional to:

Aspect Ratio (AR): High-AR wings produce less induced drag.
Speed squared ( 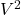$V^2$ ): Induced drag decreases rapidly with speed.

Thus, $D_i$ is dominant at low speeds and high lift conditions.

4. Total Drag Polar

The total drag coefficient ( $C_D$ ) is often expressed as:

$C_D = C_{D0} + \frac{C_L^2}{\pi e AR}$

This is known as the drag polar equation. It shows that total drag is a combination of:

A constant term: zero-lift drag ( $C_{D0}$ )
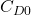A variable term: induced drag ( $\propto C_L^2$ )

5. Trade-off Between Induced and Zero-Lift Drag

At low speeds:
- Lift coefficient 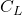$C_L$ is high → induced drag dominates.
At high speeds:
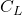- $C_L$ is low → induced drag decreases.
- Zero-lift drag increases with $V^2$ .

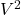There exists an optimal speed (or angle of attack) where total drag is minimized — corresponding to maximum lift-to-drag ratio ( $L/D$ ).

6. Practical Implications

Long wings (high AR): Reduce induced drag → more efficient for gliders and high-altitude UAVs.
Streamlined shapes: Reduce parasite drag → important for high-speed aircraft.
Efficient flight planning: Choose speeds where total drag is minimized (best range and endurance).

7. Summary

Drag Type	Depends On	Dominant At	Mitigation Strategies
Induced Drag	$C_L^2 / (\pi e AR)$	Low speeds	Increase aspect ratio, use winglets
Zero-Lift Drag	$C_{D0}$ , $V^2$	High speeds	Streamlined design, reduce surface area

Understanding and managing both induced and zero-lift drag is essential for optimizing aircraft performance, improving fuel efficiency, and designing efficient aerodynamic configurations.

Empowering you for GATE & Beyond
GATE 2026 | GATE 2027

Empowering you for GATE & Beyond
GATE 2026 | GATE 2027

Induced Drag & Zero-Lift Drag

1. Total Drag