Aerodynamic Forces & Moments

By /

In addition to linear forces, an aircraft experiences aerodynamic moments (torques) that influence its rotation about its center of gravity. These forces and moments arise from the distribution of pressure and shear stress over the aircraft surfaces and are central to understanding stability and control in flight mechanics.

1. Aerodynamic Forces

Aerodynamic forces act on the aircraft’s center of pressure and can be resolved into three orthogonal components relative to the flight path or body axes.

1.1 Lift (L)

  • Acts perpendicular to the relative airflow.
  • Supports the aircraft against gravity.

L = \frac{1}{2} \rho V^2 S C_L

1.2 Drag (D)

  • Acts opposite to the relative airflow.
  • Resists forward motion.

D = \frac{1}{2} \rho V^2 S C_D

1.3 Side Force (Y)

  • Acts perpendicular to both lift and drag directions.
  • Significant during sideslip or crosswind conditions.

2. Aerodynamic Moments

Aerodynamic moments tend to rotate the aircraft about its center of gravity (CG). They are critical for stability and control.

2.1 Pitching Moment (M)

  • Rotation about the lateral (y) axis.
  • Controlled by horizontal tail and elevator.
  • Defines longitudinal stability.

M = \frac{1}{2} \rho V^2 S \bar{c} C_m

Where:

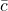  • \bar{c} = Mean aerodynamic chord
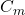  • C_m = Pitching moment coefficient

2.2 Rolling Moment (L)

  • Rotation about the longitudinal (x) axis.
  • Controlled by ailerons or spoilers.
  • Crucial for banked turns.

L = \frac{1}{2} \rho V^2 S b C_l

Where:

  • b = Wingspan
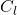  • C_l = Rolling moment coefficient

2.3 Yawing Moment (N)

  • Rotation about the vertical (z) axis.
  • Controlled by the rudder.
  • Important for directional stability.

N = \frac{1}{2} \rho V^2 S b C_n

Where:

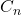  • C_n = Yawing moment coefficient

3. Moment Reference Points

  • Moments are typically computed about the aerodynamic center or the center of gravity.
  • The Aerodynamic Center (AC) is the point along the chord where the pitching moment is independent of angle of attack (for subsonic flow, usually at ~25% chord for typical airfoils).
  • The Center of Gravity (CG) location affects stability and control characteristics.

4. Stability and Control Derivatives

Aerodynamic moments depend on flight conditions and control inputs. Their variation with flight variables is quantified using stability and control derivatives.

Examples:

  • \frac{\partial C_m}{\partial \alpha}: Pitching moment change with angle of attack.
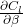  • \frac{\partial C_l}{\partial \beta}: Rolling moment change with sideslip angle.
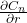  • \frac{\partial C_n}{\partial r}: Yawing moment change with yaw rate.

These derivatives are fundamental for analyzing dynamic stability and designing control systems.

5. Force and Moment Coefficient Equations

General non-dimensional expressions:

  • Lift coefficient:

C_L = \frac{L}{\frac{1}{2} \rho V^2 S}

Drag coefficient:

C_D = \frac{D}{\frac{1}{2} \rho V^2 S}

Side-force coefficient:

C_Y = \frac{Y}{\frac{1}{2} \rho V^2 S}

Pitching moment coefficient:

C_m = \frac{M}{\frac{1}{2} \rho V^2 S \bar{c}}

Rolling moment coefficient:

C_l = \frac{L}{\frac{1}{2} \rho V^2 S b}

Yawing moment coefficient:

C_n = \frac{N}{\frac{1}{2} \rho V^2 S b}

6. Summary

Aerodynamic forces and moments are critical for understanding an aircraft’s motion, stability, and control. While forces determine linear acceleration, moments cause rotation about the center of gravity. Careful analysis of these effects is essential for aircraft design, stability analysis, and flight safety.

Shopping Cart
Scroll to Top