To analyze central force motion, it is convenient to express the equations of motion in polar coordinates ![]() , since the force depends only on radial distance and points along the radius vector.
, since the force depends only on radial distance and points along the radius vector.
Position and Velocity in Polar Coordinates
The position vector in polar coordinates is:
![]()
The velocity vector is given by:
![]()
where:
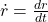 is the radial velocity.
is the radial velocity.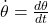 is the angular velocity.
is the angular velocity.
Acceleration in Polar Coordinates
The acceleration vector is:
![]()
It has two components:
- Radial acceleration:
![]()
Transverse (angular) acceleration:
![]()
Newton’s Second Law for Central Force
Since the central force has no transverse component:
![]()
This yields:
![]()
So:
![]()
This equation represents conservation of angular momentum. It can be integrated to give:
![]()
where ![]() is a constant (specific angular momentum per unit mass).
is a constant (specific angular momentum per unit mass).
Radial Equation of Motion
The radial component of Newton’s second law is:
![]()
Substituting:
![]()
Using ![]() , we get:
, we get:
![]()
This is the radial equation of motion for central force motion.
Summary of Equations
- Conservation of angular momentum:
![]()
Radial equation of motion:
![]()
These equations fully describe the dynamics of a particle under a central force in a plane, enabling analysis of orbital trajectories and properties.

