Conic Sections as Orbital Paths

By /

The trajectories of bodies under an inverse-square central force, such as gravity, are described by conic sections—geometric curves that include circles, ellipses, parabolas, and hyperbolas. The shape of an orbit depends on its eccentricity (e), a parameter that measures the deviation from a perfect circle.

General Equation of an Orbit

For an inverse-square central force, the orbit equation in polar coordinates is:

r(\theta) = \frac{p}{1 + e \cos(\theta - \theta_0)}

where:

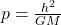  • p = \frac{h^2}{G M} is the semi-latus rectum,
  • e is the eccentricity,
  • \theta_0 defines the orientation of the orbit.

This equation shows that the path depends entirely on e and p.

Definition of Eccentricity

Eccentricity is a dimensionless parameter defined by the energy and angular momentum of the orbit:

e = \sqrt{1 + \frac{2 E h^2}{m (G M m)^2}}

where:

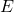  • E is the total mechanical energy,
  • h is the specific angular momentum,
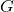  • G is the gravitational constant,
  • M is the mass of the central body.

Classification of Orbits by Eccentricity

The value of e determines the type of conic section and thus the nature of the orbit:

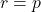  • Circle: e = 0 The orbit is a perfect circle with constant radius r = p. The body remains at a fixed distance from the center. The total energy is negative.
  • Ellipse: 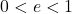0 < e < 1 Represents bounded motion. The central body lies at one focus of the ellipse. The total energy remains negative:

E < 0

Parabola: e = 1

The body follows a parabolic trajectory, representing critical escape with exactly the escape energy:

E = 0

Hyperbola: e > 1

The path is a hyperbola, indicating unbounded motion where the body escapes with excess energy:

E > 0

Geometric Parameters

  • Semi-latus rectum p determines the scale of the orbit and depends on angular momentum:

p = \frac{h^2}{G M}

Semi-major axis a for ellipses relates to energy:

E = -\frac{G M m}{2a}

where a = \frac{r_{\text{peri}} + r_{\text{apo}}}{2}.

Physical Interpretation

  • Bound Orbits: Circles and ellipses correspond to objects gravitationally bound to the central body (e.g., planets, satellites).
  • Unbound Orbits: Parabolas and hyperbolas represent objects that can escape the gravitational field (e.g., comets on escape trajectories, interstellar probes).
  • Eccentricity as Shape Measure: Low eccentricity indicates near-circular orbits, while high eccentricity describes highly elongated paths.

Examples in Celestial Mechanics

  • Earth’s orbit around the Sun: e \approx 0.0167 (nearly circular).
  • Many comets have highly elliptical or even parabolic orbits.
  • Spacecraft performing gravity assists may follow hyperbolic escape trajectories relative to planets.

By solving the general orbit equation and analyzing the value of eccentricity, we can classify and predict the shapes of all possible trajectories in a central force field.

Shopping Cart
Scroll to Top