Kepler’s Third Law (Harmonic Law)

By /

Kepler’s Third Law states:

“The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.”

This law establishes a precise mathematical relationship between the size of an orbit and the time it takes to complete one revolution.

Mathematical Form

For any planet or satellite orbiting a much more massive central body:

T^2 \propto a^3

where:

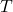  • T is the orbital period (time for one complete orbit),
  • a is the semi-major axis of the ellipse.

The proportionality constant depends on the gravitational parameter of the central body.

General Equation

Newton’s law of universal gravitation shows that for an orbit around a central mass M:

T = 2\pi \sqrt{\frac{a^3}{G M}}

where:

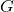  • G is the gravitational constant,
  • M is the mass of the central body (e.g., the Sun).

This equation applies to all elliptical orbits, regardless of eccentricity.

Special Case: Circular Orbit

For a circular orbit (where a = r):

T = 2\pi \sqrt{\frac{r^3}{G M}}

which is a direct application of Kepler’s Third Law to circular motion.

Implications

  • All planets around the same star share the same proportionality:

\frac{T^2}{a^3} = \text{constant}

Orbits with larger semi-major axes have longer periods.

The law allows prediction of orbital periods if a is known, or vice versa.

Example: Earth’s Orbit

  • Semi-major axis: a = 1 , \text{AU} = 1.496 \times 10^{11} , \text{m}
  • Orbital period: T = 1 , \text{year}

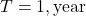
Using Kepler’s Third Law:

T^2 = \frac{4\pi^2}{G M} a^3

this relationship holds exactly for all planets orbiting the Sun.

Physical Interpretation

Kepler’s Third Law reflects the balance between gravitational attraction and orbital motion:

  • A stronger gravitational field (larger M) results in shorter periods for a given a.
  • Larger orbits take much longer to complete due to weaker gravitational acceleration.

Significance

Kepler’s Third Law unifies all planetary orbits under one simple mathematical rule. It is essential for calculating satellite periods, planning interplanetary missions, and understanding the structure of planetary systems.

Shopping Cart
Scroll to Top