Second Law of Thermodynamics

By /

The Second Law of Thermodynamics introduces the concept of irreversibility and defines the direction of energy transfer. While the First Law accounts for conservation of energy, it does not tell us whether a process is feasible. The Second Law provides criteria for the spontaneity of processes and is crucial for understanding the performance limits of aircraft engines.

1. Basic Statement of the Second Law

The Second Law can be stated in several ways. Two classical statements are:

  • Kelvin-Planck Statement: It is impossible to construct a device that operates in a cycle and produces no effect other than the conversion of heat from a single reservoir into equivalent work.
  • Clausius Statement: It is impossible to construct a device that operates in a cycle and transfers heat from a colder body to a hotter body without external work.

These statements imply that not all heat can be converted to work, setting fundamental limits on engine efficiency.

2. Entropy

The Second Law introduces the property entropy (S), a measure of disorder or randomness in a system. For a reversible process:

dS = \frac{\delta Q_{rev}}{T}

For an irreversible process:

dS > \frac{\delta Q}{T}

Entropy change indicates the amount of energy unavailable for work. In a closed system undergoing a process:

\Delta S_{system} + \Delta S_{surroundings} \geq 0

Equality holds for reversible processes, while inequality indicates irreversibility.

3. Entropy Balance for Control Volumes

In aircraft engines, which are open systems, the entropy balance for a steady-flow control volume is:

\dot{m}<em>{in} s</em>{in} - \dot{m}<em>{out} s</em>{out} + \frac{\dot{Q}}{T_{boundary}} = \dot{S}_{gen}

Where:

  • \dot{m} = mass flow rate
  • s = specific entropy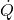
  • \dot{Q} = heat transfer rate
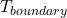  • T_{boundary} = temperature at the boundary where heat transfer occurs
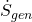  • \dot{S}_{gen} = rate of entropy generation (always ≥ 0)

Entropy generation represents irreversibilities due to friction, unrestrained expansion, heat transfer across finite temperature differences, and mixing.

4. Implications for Aircraft Propulsion

Irreversibilities reduce the efficiency of propulsion systems. In an ideal engine (reversible processes), entropy generation is zero, maximizing work output. However, real engines have:

  • Friction in turbines and compressors
  • Pressure losses in ducts and combustors
  • Heat transfer across temperature gradients

These irreversibilities increase entropy, reducing the fraction of heat energy that can be converted to useful work. Engineers strive to minimize these losses through careful design.

5. Thermal Efficiency Limit: Carnot Efficiency

The Second Law defines the maximum theoretical efficiency of any heat engine operating between two reservoirs:

\eta_{Carnot} = 1 - \frac{T_C}{T_H}

Where:

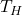  • T_H = temperature of the hot reservoir
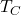  • T_C = temperature of the cold reservoir

No real engine can exceed this efficiency. In gas turbine engines, increasing the turbine inlet temperature (T_H) improves efficiency but is limited by material capabilities.

6. Practical Application in Jet Engines

  • Compressor: Ideally isentropic, but real compression generates entropy.
  • Combustor: Heat addition at high temperature increases entropy.
  • Turbine: Ideally isentropic expansion, but real processes have losses.
  • Nozzle: Expansion accelerates gases, ideally with minimal entropy generation.

By applying the Second Law to each component, engineers can analyze and improve engine performance, aiming to reduce entropy generation wherever possible.

Shopping Cart
Scroll to Top