1. Introduction
In solid mechanics, simplifying a three-dimensional stress or strain state to a two-dimensional approximation is often valid and practical, especially in aerospace structural analysis. Two such common idealizations are:
- Plane Stress – Suitable for thin flat elements like aircraft skins.
- Plane Strain – Applicable to long structural members where deformation in one direction is restricted.
2. Plane Stress Condition
2.1 Assumptions
Plane stress assumes negligible stress in the thickness direction (say, zz-axis):
![]()
Non-zero stress components:
![]()
2.2 Strain Relations
The 3D strain–stress relations reduce to:
![]()
![]()
![]()
![]()
Where:
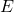 = Young’s modulus
= Young’s modulus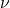 = Poisson’s ratio
= Poisson’s ratio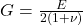 = Shear modulus
= Shear modulus
3. Plane Strain Condition
3.1 Assumptions
Plane strain assumes zero strain in the zz-direction:
![]()
Non-zero strain components:
![]()
Typical in long bodies where the length dimension is constrained (e.g., long fuselage sections or nozzles).
3.2 Stress–Strain Relations
From Hooke’s law in 3D:
![]()
![]()
![]()
Solving for ![]() :
:
![]()
So, out-of-plane stress is non-zero, even though ![]() .
.
4. Effective Elastic Moduli (Plane Strain)
In many numerical methods (like FEM), plane strain uses modified elastic constants:
- Effective Young’s Modulus:
![]()
Effective Poisson’s Ratio:
![]()
5. Comparison Table
| Feature | Plane Stress | Plane Strain |
|---|---|---|
| Common Scenario | Thin plates, aircraft skins | Long, constrained structures |
| Governing Equations | 2D Hooke’s Law | Modified 3D Hooke’s Law |
6. Relevance in Aerospace Applications
- Plane Stress:
- Used for thin sheets under in-plane loads (e.g., fuselage skins, wing panels).
- Critical in analyzing riveted and composite skin structures.
- Plane Strain:
- Found in long aerospace structures where end constraints dominate (e.g., nozzle flanges, spars under axial compression).
- Also relevant in structural dynamic simulations where transverse motion is minimal.

