1. Introduction to Structural Members
Beams are fundamental structural elements designed to resist loads applied perpendicular to their longitudinal axis. The study of how point loads affect beams is critical in understanding responses such as support reactions, internal shear forces, and bending moments.
1.1 Definition: Point Load
A point load (or concentrated load) is a force applied at a single, specific location along the beam. In practice, true point loads are idealizations, as real loads act over finite areas; nonetheless, the point load model is useful for analysis of structural elements.
2. Types of Beams and Supports
2.1 Common Beam Types
- Simply Supported Beam: Supported at both ends, allowing rotation but not translation.
- Cantilever Beam: Fixed at one end, free at the other.
- Overhanging Beam: Extends beyond its supports at one or both ends.
2.2 Support Types
- Pinned Support: Allows rotation, restricts translation.
- Roller Support: Allows rotation and horizontal translation, restricts vertical movement.
- Fixed Support: Restricts translation and rotation.
3. Analysis of Point Loads on Beams
3.1 Reactions at Supports
Goal: To determine the reactions at the supports due to a given point load.
Example Problem 1: Simply Supported Beam with a Single Point Load
Consider a beam of length L, simply supported at both ends, with a point load P applied at a distance a from the left support.
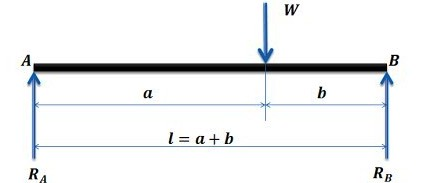
Step 1: Free Body Diagram (FBD)
- Draw the beam, mark support points A (left) and B (right).
- Apply point load P at distance a from A, L – a from B.
Step 2: Equilibrium Equations
- Sum of vertical forces:
![]()
Sum of moments about A:
![]()
Step 3: Solve for Reactions
- From moments:
![]()
Substitute in vertical force equation:
![]()
Table: Support Reactions
| Support | Reaction Formula |
|---|---|
| Left | |
| Right |
4. Shear Force and Bending Moment
4.1 Shear Force Diagram (SFD)
A shear force at a section is the sum of vertical forces to the left or right of the section. It experiences a sudden change (jump) at the location of the point load.
- Left of point load: Shear force is
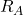 .
. - Right of point load: Shear force is
 .
.
SFD Construction Steps:
- Start from left end at
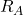 .
. - Drop by
 at the load location.
at the load location. - Continue at
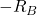 to the right end.
to the right end.
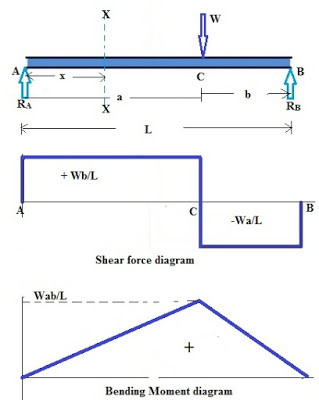
4.2 Bending Moment Diagram (BMD)
The bending moment at a section is the sum of moments about that section due to forces on one side.
- For location x<ax < ax<a:
![]()
For location x>ax > ax>a:
![]()
Maximum Bending Moment under the point load (x=ax = ax=a):
![]()
5. Worked Example
Example Problem
Given: Simply supported beam, L=6 m, point load P=10 kN at a=2 m from the left support.
Solution:
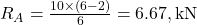
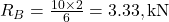
- Max bending moment:
![]()
6. Summary Table: Key Formulas for Point Loads on Beams
| Quantity | Formula |
|---|---|
| Reaction at left support | |
| Reaction at right support | |
| Shear just left of load | |
| Shear just right of load | |
| Max bending moment (under P) | |
| Bending moment at section x | |
7. Interpretation and Physical Significance
- At the application point of a load, shear force exhibits a discontinuity (jump).
- Bending moment profile is piecewise linear, with the maximum under the point load.
- These insights are essential for structural design and safety assessments.

