Statically Indeterminate Trusses and Beams

1. Introduction

A statically indeterminate structure is one where the number of unknown forces (reactions or internal forces) exceeds the number of available equilibrium equations. Unlike statically determinate structures, which can be solved using only the equations of equilibrium, indeterminate structures require additional conditions — such as compatibility of deformation — and often invoke methods based on material behavior (like Hooke’s Law or strain energy concepts).

This chapter focuses on understanding such indeterminate behavior in both trusses and beams.

---

2. Degree of Indeterminacy

The degree of static indeterminacy (DSI) is given by:

• For planar trusses:
  
  where:
  • = number of members
  • = number of support reactions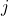
  • = number of joints
• For beams and frames:
  (in 2D)
  (assuming 3 equilibrium equations available)

If , the structure is statically indeterminate.

---

3. Statically Indeterminate Trusses

3.1 Characteristics

• Cannot be solved by equilibrium equations alone
• Require compatibility conditions (displacement continuity)
• Common in redundant or highly rigid aerospace frameworks

3.2 Method of Analysis

• Method of Consistent Deformations (Force Method):
  • Choose redundant forces and remove them temporarily
  • Solve the remaining determinate structure
  • Apply compatibility conditions to find redundant forces

Steps:

1. Identify the redundant member(s)
2. Analyze the basic determinate structure
3. Use virtual work (unit load method) or deformation formulas
4. Solve compatibility equations

3.3 Example:

Problem:
A simple truss consists of a triangle (3 joints, 3 members), with an extra diagonal added. Determine internal forces using force method.

→ 1 degree statically indeterminate

Remove diagonal → analyze basic truss → compute displacement at redundant location → solve for redundant force

---

4. Statically Indeterminate Beams

4.1 Characteristics

• More supports or internal constraints than needed for equilibrium
• Cannot solve using just
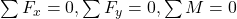
• Requires deflection compatibility (e.g., same slope or displacement at certain points)

4.2 Methods of Analysis

• Force (Flexibility) Method
• Moment Area Method
• Three-Moment Equation (for continuous beams)
• Slope-Deflection Method
• Direct Stiffness or Matrix Methods (advanced)

---

5. Force Method – General Approach

Steps:

1. Identify the indeterminacy (number of redundant forces)
2. Remove enough redundants to make the structure determinate
3. Solve for reactions/displacements using:
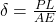   • (axial)
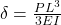   • (bending)
4. Impose compatibility equations (total displacement = 0 at redundant)

---

6. Example – Fixed Beam

Problem:
A fixed beam of length carries a uniformly distributed load over the entire span.

DSI = 2 (fixed beam → 4 reactions; equilibrium → 2 equations)

Use compatibility of rotations and deflections:

• Assume reaction moments at supports
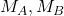
• Use standard deflection formula: θ=∫M(x)EIdx\theta = \int \frac{M(x)}{EI} dx
• Set net rotation at both ends = 0

Final Results (from standard case):

Maximum BM at center:

---

7. Continuous Beams – The Three-Moment Equation

This method is applicable for continuous beams over multiple supports.

Equation: M1L1+2M2(L1+L2)+M3L2=−6(A1L1+A2L2)M_1 L_1 + 2 M_2 (L_1 + L_2) + M_3 L_2 = -6 \left( \frac{A_1}{L_1} + \frac{A_2}{L_2} \right)

where:

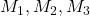• = moments at supports
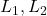• = adjacent spans
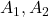• = areas under the bending moment diagrams for UDLs or loads between supports

---

8. Applications in Aerospace Structures

In aircraft design, redundancy is often desirable for safety and reliability. Wings, fuselage panels, and load-bearing structures are often statically indeterminate to ensure load redistribution in case of local failure. Analysis helps predict structural response more accurately than with idealized statically determinate models.

---

9. Summary

Type	Characteristic	Method Used
Truss	DSI > 0, extra members	Force method, compatibility
Beam	Extra supports/constraints	Moment-area, 3-moment, slope-deflection
Frame	Combination	Matrix methods