1. Introduction
Unlike point loads that act at a single location, uniform loads are distributed evenly along a portion or the entire length of a beam. These are referred to as uniformly distributed loads (UDL) and are common in real-world aerospace structures. For instance:
- The weight of the aircraft wing skin and fuel tanks,
- Aerodynamic lift acting as distributed upward loads,
- Continuous pressure from attached components or insulation.
Understanding the behavior of beams under uniform loading is essential to evaluate bending and shear responses, size structural members, and ensure reliability under sustained loading.
2. Definition of Uniformly Distributed Load (UDL)
A UDL has constant intensity ![]() (force per unit length) applied over a length of beam.
(force per unit length) applied over a length of beam.
- Units:
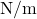 or
or 
- Total load over length
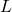 is
is 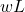
- Acts over the centroid of the distribution — i.e., at the center of the span
3. Analysis of Simply Supported Beam under UDL
Let’s analyze a beam of length ![]() simply supported at ends A and B with a UDL of intensity
simply supported at ends A and B with a UDL of intensity ![]() acting over the entire span.
acting over the entire span.
Support Reactions
By symmetry and equilibrium:
![]()
Shear Force (V)
Shear force at a distance ![]() from the left support:
from the left support:
![]()
- Linearly decreases from
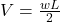 at
at 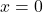 to
to 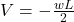 at
at 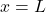
- Shear force becomes zero at midspan

Bending Moment (M)
Bending moment at distance ![]() from the left support:
from the left support:
![]()
Maximum bending moment occurs at ![]() :
:
![]()
4. Cantilever Beam under UDL
For a cantilever beam of length ![]() fixed at one end and subjected to a UDL
fixed at one end and subjected to a UDL ![]() over the entire length:
over the entire length:
Support Reactions
- Vertical reaction at fixed end:
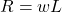
- Fixed-end moment:
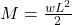
Shear Force (V)
At any point ![]() from the fixed end:
from the fixed end:
![]()
- Shear varies linearly from
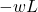 at fixed end to
at fixed end to 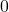 at free end.
at free end.
Bending Moment (M)
![]()
- Maximum moment at fixed end:
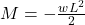
- Moment decreases quadratically to zero at the free end.
5. Key Observations
- Shear Force Diagram (SFD): Linear in UDL; slope equals load intensity
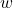
- Bending Moment Diagram (BMD): Parabolic in UDL; curvature due to distributed nature of loading
- Maximum moment and shear depend on span and load intensity
6. Practical Examples in Aerospace
- Distributed weight of wing components or passengers
- Uniform aerodynamic lift along a wing span
- Pressure load from pressurization systems in fuselage sections
These loads are rarely point-concentrated, making UDL analysis especially relevant in preliminary design and structural verification phases.
7. Superposition Principle
If a beam carries multiple UDLs, or combinations of UDL and point loads:
- Compute individual effects for each load case
- Use superposition to obtain net shear force and moment distributions
8. Summary of Equations
| Quantity | Simply Supported Beam | Cantilever Beam |
|---|---|---|
| Max Shear | ||
| Max Moment |

