Varying Loads on Beams

By /

1. Introduction

While point loads and uniformly distributed loads (UDL) are idealized loadings, varying distributed loads (also called non-uniform or linearly varying loads) more closely represent real-world aerospace applications. These loads vary in intensity along the length of the beam and are frequently encountered in structures such as:

  • Wings with elliptic lift distribution
  • Pressure differentials in fuselage skins
  • Tapered payload or equipment support beams

Understanding how to analyze beams under varying loads is essential for accurately predicting internal forces and designing for safety.

2. Types of Varying Loads

2.1. Linearly Varying Loads

Most common type — load intensity increases or decreases linearly from one end to another. Represented as a triangular load distribution.

  • Starts from zero and increases to 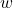w over a span 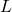L, or vice versa.
  • Load intensity as a function of position x:
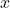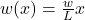    w(x) = \frac{w}{L}x (if starting from zero)

2.2. Trapezoidal Loads

Combination of uniform and linearly varying loads.

3. Total Load and Point of Action

For a triangular load of peak intensity w over length L:

  • Total Load = Area under load diagram =

W = \frac{1}{2}wL

Point of Action = Located at \frac{L}{3} from the higher intensity side (or \frac{2L}{3} from the zero side)

4. Example: Simply Supported Beam with Triangular Load

Let a simply supported beam of length L carry a triangular load increasing from zero at A to w at B.

Support Reactions

Using static equilibrium:

  • Total load: W = \frac{1}{2}wL
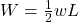
  • Load acts at 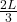\frac{2L}{3} from A
  • Reactions:

R_A = \frac{1}{6}wL

R_B = \frac{1}{3}wL

Shear Force (V)

To find shear force at distance x, integrate load intensity:

w(x) = \frac{w}{L}x
Shear force:

V(x) = R_A - \int_0^x w(x),dx = \frac{1}{6}wL - \int_0^x \frac{w}{L}x,dx = \frac{1}{6}wL - \frac{w x^2}{2L}

Bending Moment (M)

Bending moment is the integral of shear:

M(x) = \int_0^x V(x),dx = \int_0^x \left(\frac{1}{6}wL - \frac{w x^2}{2L} \right)dx = \frac{1}{6}wLx - \frac{w x^3}{6L}

  • Maximum bending moment occurs where shear force is zero.
  • Set 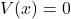V(x) = 0, solve for x.

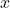5. Cantilever Beam under Varying Load

Let’s take a cantilever beam with triangular load decreasing from w at fixed end to 0 at free end:

  • Total load: W = \frac{1}{2}wL
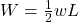
  • Location of resultant: \frac{L}{3} from fixed end

Shear Force:

V(x) = - \int_0^x w(x),dx = - \int_0^x w \left(1 - \frac{x}{L}\right),dx = -wx + \frac{w x^2}{2L}

Bending Moment:

M(x) = - \int_0^x V(x),dx = - \int_0^x \left(-wx + \frac{w x^2}{2L} \right)dx = \frac{w x^2}{2} - \frac{w x^3}{6L}

At the fixed end (x = L):

M_{\text{max}} = \frac{wL^2}{2} - \frac{wL^3}{6L} = \frac{wL^2}{3}

6. Shear Force and Bending Moment Diagrams

  • Shear Force Diagram (SFD): Parabolic for triangular loads
  • Bending Moment Diagram (BMD): Cubic shape

These diagrams help in identifying maximum internal stresses and are essential for sizing cross-sections and supports.

7. Real-Life Aerospace Examples

  • Lift distribution over an elliptical or tapered wing
  • Pressure variation across a non-uniform fuselage skin
  • Gradual load transfer through tapered composite members

8. Summary

Load TypeTotal LoadCentroid (from smaller end)
Triangular\frac{1}{2}wL\frac{2L}{3}
TrapezoidalCombine UDL + triangularUse centroid formulas

Understanding the effects of varying loads is essential for precise structural design and weight optimization in aerospace systems.

Shopping Cart
Scroll to Top