1. Introduction
Understanding how internal forces and moments vary along the length of a beam is essential for designing safe and efficient aerospace structures. The two key internal quantities are:
- Shear Force (V): The internal force perpendicular to the beam axis at a cross-section.
- Bending Moment (M): The internal moment that causes bending at a section of the beam.
These quantities vary from point to point and can be graphically represented using Shear Force Diagrams (SFD) and Bending Moment Diagrams (BMD).
2. Sign Convention
A consistent sign convention helps ensure correct diagrams:
- Shear Force:
- Positive when the left segment tends to move upward relative to the right segment.
- Bending Moment:
- Positive (sagging) when the beam tends to bend in a U-shape (concave upward).
- Negative (hogging) when it bends in an inverted U-shape (concave downward).
3. Relationship Between Load, Shear, and Moment
For a beam with distributed load ![]() :
:
![]()
![]()
These equations imply:
- Shear force is the slope of the moment diagram.
- Load intensity is the negative slope of the shear force diagram.
This differential relationship allows you to sketch SFD and BMD from loading information or vice versa.
4. Key Features of SFD and BMD
- A point load causes a jump in shear force, but a corner (discontinuity in slope) in the bending moment.
- A uniformly distributed load (UDL) causes a linear change in shear and a quadratic curve in moment.
- A point moment causes a jump in bending moment but no effect on shear.
5. Procedure to Draw SFD and BMD
- Find support reactions using static equilibrium.
- Divide the beam into segments between load changes.
- Write expressions for
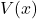 and
and  in each segment.
in each segment. - Plot values at key points (supports, load points, zero crossings).
- Join points with correct curvature based on load types.
6. Example: Simply Supported Beam with Point Load
A beam of length ![]() has a point load
has a point load ![]() at the midpoint.
at the midpoint.
Step 1: Reactions
Symmetric case ⇒
![]()
Step 2: Shear Force
- From
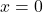 to
to 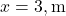 :
:
![]()
At ![]() (point load):
(point load):
![]()
From ![]() to
to ![]() :
:
![]()
Step 3: Bending Moment
- From
 :
:
![]()
From ![]() :
:
![]()
Maximum bending moment at center:
![]()
Sketch (Description):
- SFD: A horizontal line at +6 kN until midspan, sudden drop to -6 kN, then constant.
- BMD: A triangle with peak at 18 kNm at midspan, symmetric.
7. Example: Cantilever with UDL
A cantilever beam of length ![]() carries a UDL of
carries a UDL of ![]() .
.
Step 1: Reactions
At fixed end:
![]()
![]()
Step 2: Shear Force
![]()
Step 3: Bending Moment
![]()
Sketch (Description):
- SFD: Linear variation from -8 kN at support to 0 at free end.
- BMD: Quadratic curve from -16 kNm at support to 0 at free end.
8. Interpretation for Aerospace Applications
- Aircraft wing spars, fuselage frames, and undercarriage supports often behave like beams.
- Predicting shear and moment helps locate critical points of failure.
- Overdesign at peak moment points prevents catastrophic buckling or cracking.
9. Summary
- Shear force and bending moment diagrams reveal internal force variation.
- Point loads → step in shear, corner in moment.
- Distributed loads → sloped shear, curved moment.
- Use equilibrium and calculus to generate SFD and BMD systematically.

