Bernoulli’s Equation

By /

Bernoulli’s principle is one of the most famous and widely used results in fluid mechanics. It explains how pressure, velocity, and elevation are related along a streamline in a steady, incompressible, inviscid flow.

It is derived from the conservation of energy applied to flowing fluids and provides powerful insights for aerodynamics, engineering, and everyday phenomena.

1️⃣ Physical Meaning of Bernoulli’s Principle

Bernoulli’s principle states:

In steady, incompressible, inviscid flow along a streamline, the sum of pressure energy, kinetic energy, and potential energy per unit weight is constant.

Intuitively:

  • If fluid speeds up, its pressure drops.
  • If fluid slows down, its pressure rises.

This principle explains why airplane wings generate lift, how carburetors mix fuel and air, and why a shower curtain gets sucked inward when water flows.

2️⃣ Bernoulli’s Equation (General Form)

For steady, incompressible, inviscid flow with gravity effects:

\frac{p}{\rho} + \frac{V^2}{2} + gz = \text{constant}

Where:

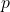  • p : static pressure (Pa)
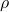  • \rho : fluid density (kg/m³)
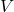  • V : flow velocity (m/s)
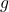  • g : gravitational acceleration (m/s²)
  • z : elevation above a reference level (m)

Explanation:

  • \frac{p}{\rho} : pressure head (energy per unit mass due to pressure)
  • \frac{V^2}{2} : velocity head (kinetic energy per unit mass)
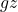  • gz : potential head (potential energy per unit mass)

3️⃣ Simplified Horizontal Flow (No Elevation Change)

In many aerodynamic and engineering cases, elevation changes are negligible (flat ducts, airfoils at small angles):

\frac{p}{\rho} + \frac{V^2}{2} = \text{constant}

Key idea:

  • Increase in velocity leads to decrease in pressure.
  • Decrease in velocity leads to increase in pressure.

4️⃣ Derivation from Energy Conservation

Bernoulli’s equation can be derived from the steady flow energy equation under these assumptions:

✅ Steady flow
✅ Incompressible fluid
✅ Inviscid (no viscosity)
✅ Along a streamline
✅ No shaft work or heat transfer

Under these conditions, the energy equation simplifies to Bernoulli’s form.

5️⃣ Example 1: Flow Through a Constriction

Consider horizontal pipe flow with a narrowing section:

Given:

  • Inlet area 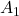A_1 , velocity 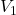V_1 , pressure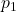 p_1
  • Throat area 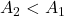A_2 < A_1 , velocity 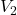V_2 , pressure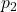 p_2

Continuity Equation:

A_1 V_1 = A_2 V_2

Bernoulli’s Equation (horizontal):

\frac{p_1}{\rho} + \frac{V_1^2}{2} = \frac{p_2}{\rho} + \frac{V_2^2}{2}

Result:

A_2 < A_1 \Rightarrow V_2 > V_1

So p_2 < p_1

Interpretation:

  • The fluid speeds up in the constriction.
  • Pressure drops in the constriction.

Application: Venturi meter for flow measurement.

6️⃣ Example 2: Pitot-Static Tube (Airspeed Measurement)

Used on aircraft to measure airspeed:

  • Stagnation point (where flow stops): velocity = 0, pressure = p_0 (stagnation pressure)
  • Free stream: velocity = 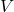V , pressure =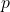 p

Bernoulli’s Equation:

\frac{p_0}{\rho} = \frac{p}{\rho} + \frac{V^2}{2}

Solve for velocity:

V = \sqrt{\frac{2(p_0 - p)}{\rho}}

Interpretation:

  • Measures airspeed using pressure difference.
  • Essential in aviation instrumentation.

7️⃣ Example 3: Lift on an Airfoil

  • Airfoil shape accelerates flow over the top surface.
  • By Bernoulli’s principle, higher velocity leads to lower pressure on top.
  • Pressure difference generates lift.

Simplified Analysis:

  • Over top: V_{\text{top}} > V_{\text{bottom}}
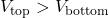
  • So: p_{\text{top}} < p_{\text{bottom}}
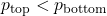
  • Resulting net upward force (lift).

8️⃣ Applications in Aerodynamics and Engineering

✅ Aircraft Wings: Lift generation from pressure differences.
✅ Venturi Meters: Measuring flow rate in pipes.
✅ Carburetors: Mixing fuel and air via low-pressure regions.
✅ Wind Tunnels: Testing models using known pressure-velocity relationships.
✅ Diffusers and Nozzles: Controlling flow speed and pressure in engines.
✅ Hydraulic Engineering: Spillways and flow measurement.

9️⃣ Limitations of Bernoulli’s Principle

Bernoulli’s equation relies on simplifying assumptions:

❌ Inviscid flow (no viscosity).
❌ Steady flow.
❌ Incompressible flow (constant density).
❌ Along a streamline.
❌ No heat or work interactions.

Real-world flows may include:

  • Viscous losses (boundary layers, turbulence).
  • Compressibility effects (shock waves at high speeds).
  • Heat addition (combustion in engines).

For such cases, more general forms (energy equation, Navier–Stokes equations) are used.

Shopping Cart
Scroll to Top