Generalized Hooke’s Law and Elastic Constants

By /

The relationship between stress and strain in elastic materials is central to the study of solid mechanics and structural analysis. Hooke’s Law provides a linear relation between stress and strain within the elastic limit of the material. When extended to three dimensions, it becomes the generalized Hooke’s law, incorporating multiple components of stress and strain, and relating them through material-specific constants known as elastic constants.

These formulations are essential for designing and analyzing aircraft components that are subjected to multi-axial loading conditions.

1. Introduction to Hooke’s Law

In its simplest 1D form, Hooke’s Law states:

\sigma = E \varepsilon

Where:

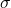  • \sigma = normal stress (N/m²),
  • \varepsilon = normal strain (dimensionless),
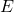  • E = Young’s modulus or modulus of elasticity (Pa).

This equation holds only within the elastic range, where the material returns to its original shape upon unloading.

2. Stress and Strain Components in 3D

In three dimensions, both stress and strain are represented as second-order tensors. Each contains 9 components, but due to symmetry in both tensors, only 6 independent components are needed to fully describe the state at a point.

2.1 Stress Tensor

\left[ \sigma \right] = \begin{bmatrix} \sigma_x & \tau_{xy} & \tau_{xz} \ \tau_{yx} & \sigma_y & \tau_{yz} \ \tau_{zx} & \tau_{zy} & \sigma_z \end{bmatrix}

2.2 Strain Tensor (Engineering strain form)

\left[ \varepsilon \right] = \begin{bmatrix} \varepsilon_x & \gamma_{xy}/2 & \gamma_{xz}/2 \ \gamma_{xy}/2 & \varepsilon_y & \gamma_{yz}/2 \ \gamma_{xz}/2 & \gamma_{yz}/2 & \varepsilon_z \end{bmatrix}

Here, \gamma_{xy}, \gamma_{yz}, and \gamma_{xz} are engineering shear strains (not tensorial strains).

3. Generalized Hooke’s Law for Isotropic Materials

For isotropic and linear elastic materials, stress and strain components are linearly related through two independent material constants:

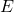  • E (Young’s Modulus),
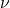  • \nu (Poisson’s Ratio).

The 3D generalized Hooke’s Law is:

3.1 Normal Strains

\varepsilon_x = \frac{1}{E} \left[ \sigma_x - \nu (\sigma_y + \sigma_z) \right]

\varepsilon_y = \frac{1}{E} \left[ \sigma_y - \nu (\sigma_z + \sigma_x) \right]

\varepsilon_z = \frac{1}{E} \left[ \sigma_z - \nu (\sigma_x + \sigma_y) \right]

3.2 Shear Strains

\gamma_{xy} = \frac{\tau_{xy}}{G}, \quad \gamma_{yz} = \frac{\tau_{yz}}{G}, \quad \gamma_{zx} = \frac{\tau_{zx}}{G}

Where G is the shear modulus, related to E and \nu by:

G = \frac{E}{2(1 + \nu)}

4. Elastic Constants and Their Relationships

A linear, isotropic material has four common elastic constants:

ConstantDescriptionUnits
EYoung’s ModulusPa
\nuPoisson’s Ratiodimensionless
GShear ModulusPa
KBulk ModulusPa

These are interrelated through the following equations:

  • Shear modulus:

G = \frac{E}{2(1 + \nu)}

Bulk modulus:

K = \frac{E}{3(1 - 2\nu)}

Thus, knowing any two of these constants allows you to compute the others.

5. Matrix Form of Generalized Hooke’s Law

In engineering notation, the stress-strain relationship can be expressed compactly in matrix form:

\begin{bmatrix} \varepsilon_x \ \varepsilon_y \ \varepsilon_z \ \gamma_{xy} \ \gamma_{yz} \ \gamma_{zx} \end{bmatrix}</h1> \frac{1}{E} \begin{bmatrix} 1 & -\nu & -\nu & 0 & 0 & 0 \ -\nu & 1 & -\nu & 0 & 0 & 0 \ -\nu & -\nu & 1 & 0 & 0 & 0 \ 0 & 0 & 0 & 2(1+\nu) & 0 & 0 \ 0 & 0 & 0 & 0 & 2(1+\nu) & 0 \ 0 & 0 & 0 & 0 & 0 & 2(1+\nu) \end{bmatrix} \begin{bmatrix} \sigma_x \ \sigma_y \ \sigma_z \ \tau_{xy} \ \tau_{yz} \ \tau_{zx} \end{bmatrix}

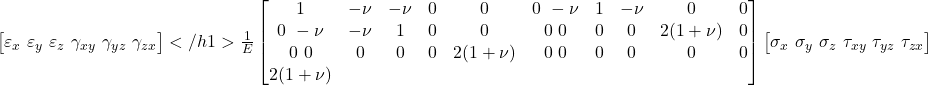
This is known as the compliance matrix. Its inverse is the stiffness matrix, used in finite element analysis.

6. Uniaxial Loading Example

Consider a rod subjected to uniaxial tensile stress \sigma_x.

  • Axial strain:

\varepsilon_x = \frac{\sigma_x}{E}

Transverse strain:

\varepsilon_y = \varepsilon_z = -\nu \frac{\sigma_x}{E}

The negative sign indicates that the material contracts laterally when stretched axially.

7. Applications in Aerospace Structures

In aircraft components such as:

  • Thin-walled fuselages under pressurization,
  • Wing skins under shear and bending,
  • Riveted joints and stringers,

…the materials are assumed to behave elastically under normal service loads. Therefore, the generalized Hooke’s law provides the first step in stress-strain analysis.

Composite materials, which are anisotropic, require a modified version of Hooke’s Law with different stiffnesses in each direction.

8. Summary

  • Hooke’s Law provides a linear relation between stress and strain in elastic materials.
  • The generalized form accounts for multiaxial loading and includes Poisson effects.
  • Key elastic constants include E, ν, G, and K, which are mathematically interrelated.
  • This framework is foundational to structural analysis, material behavior modeling, and failure prediction in aerospace engineering.
Shopping Cart
Scroll to Top