Introduction to Compressible Flow

By /

Compressible flow is the study of fluid motion where variations in fluid density are significant. In aircraft propulsion, this is essential because air and combustion gases often flow at high velocities, leading to density changes that affect engine performance.

1. Importance of Compressibility

Unlike incompressible flow (where density is constant), compressible flow considers changes in:

  • Density
  • Temperature
  • Pressure

These variations are crucial in components such as:

  • Intakes (diffusers)
  • Compressors
  • Combustion chambers
  • Turbines
  • Nozzles

For example, as air passes through a converging-diverging nozzle, it accelerates to supersonic speeds, with density and temperature dropping significantly.

2. Mach Number

A central concept in compressible flow is the Mach number (M), defined as:

M = \frac{V}{a}

Where:

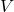  • V = local flow velocity
  • a = local speed of sound

The speed of sound in a perfect gas is:

a = \sqrt{\gamma R_s T}

Where:

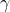  • \gamma = ratio of specific heats
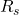  • R_s = specific gas constant
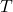  • T = temperature

Flow regimes:

  • Subsonic: M < 1
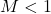
  • Transonic: M \approx 1
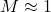
  • Supersonic: M > 1
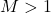
  • Hypersonic: M \geq 5

3. Compressibility Effects

As Mach number increases, compressibility effects become pronounced:

  • Density changes cannot be neglected.
  • Pressure variations significantly affect flow properties.
  • Temperature changes arise due to compression or expansion.

In propulsion systems, these effects are vital for:

  • Intake design: slowing and compressing air with minimal losses.
  • Nozzle design: accelerating exhaust gases to produce thrust.

4. Isentropic Flow Relations

For ideal, isentropic (adiabatic, reversible) flow, key relations connect pressure, temperature, and density changes to Mach number.

Temperature relation:

\frac{T}{T_0} = \frac{1}{1 + \frac{\gamma - 1}{2} M^2}

Pressure relation:

\frac{p}{p_0} = \left( \frac{T}{T_0} \right)^{\frac{\gamma}{\gamma - 1}}

Density relation:

\frac{\rho}{\rho_0} = \left( \frac{T}{T_0} \right)^{\frac{1}{\gamma - 1}}

Where:

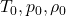  • T_0, p_0, \rho_0 = stagnation (total) properties
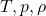  • T, p, \rho = static properties

These relations are critical for designing components that efficiently manage compressible flow.

5. Stagnation Properties

Stagnation (total) properties are conditions a flow would attain if brought to rest isentropically.

  • Stagnation temperature:

T_0 = T \left( 1 + \frac{\gamma - 1}{2} M^2 \right)

  • Stagnation pressure:

p_0 = p \left( 1 + \frac{\gamma - 1}{2} M^2 \right)^{\frac{\gamma}{\gamma - 1}}

These quantities remain constant through isentropic, adiabatic processes without work or heat addition (e.g., ideal diffusers and nozzles).

6. Area-Mach Number Relation

In nozzles and diffusers, the Area-Mach number relation governs how flow accelerates or decelerates:

\frac{dA}{A} = (M^2 - 1) \frac{dV}{V}

  • For subsonic flow (M < 1): decreasing area accelerates flow.
  • For supersonic flow (M > 1): increasing area accelerates flow.

This principle underpins the design of converging-diverging (C-D) nozzles in jet engines and rockets.

7. Normal Shock Waves

In supersonic flow, sudden compression can cause normal shocks, with abrupt changes in properties:

  • Flow decelerates from supersonic to subsonic.
  • Pressure, temperature, and density increase.
  • Total pressure drops (irreversible loss).

Shock waves are critical in:

  • Supersonic inlets (preventing engine stall)
  • High-speed nozzle design

8. Applications in Aircraft Propulsion

Compressible flow analysis is essential for:

  • Designing intakes that decelerate and compress air efficiently.
  • Modeling compressors (high-speed blades create compressible effects).
  • Analyzing combustion chambers with high-pressure flows.
  • Designing nozzles to accelerate exhaust gases for thrust.
  • Understanding shock interactions in supersonic and hypersonic flight.

9. Summary

Compressible flow concepts provide the tools to:

  • Predict how gases respond to changes in area, pressure, and temperature.
  • Design components that control velocity and pressure changes.
  • Maximize efficiency and thrust in aircraft propulsion systems.

Mastering these principles is vital for engineers working on jet engines, rockets, and high-speed aerodynamics.

Shopping Cart
Scroll to Top