Range

By /

Range is the maximum distance an aircraft can fly on a given amount of fuel. In aircraft propulsion analysis, range connects the engine’s efficiency with the aircraft’s aerodynamics and fuel capacity, making it a key measure of operational capability.

1. Definition of Range

Range is calculated as:

\text{Range} = \text{Cruise Speed} \times \text{Endurance}

Where:

  • Cruise speed is the steady flight speed.
  • Endurance is the total time the aircraft can fly on available fuel.

For jet aircraft, range depends on how efficiently the propulsion system converts fuel into thrust and how effectively that thrust overcomes drag.

2. Breguet Range Equation for Jet Aircraft

A standard model for estimating jet aircraft range is the Breguet range equation:

R = \frac{V}{\text{TSFC}} \frac{L}{D} \ln \frac{W_{initial}}{W_{final}}

Where:

  • R = range (m or km)
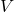  • V = cruise speed (m/s)
  • TSFC = thrust-specific fuel consumption (kg/N·s)
  • \frac{L}{D} = lift-to-drag ratio
  • W_{initial} = weight at start of cruise
  • W_{final} = weight at end of cruise

3. Explanation of Terms

  • Cruise Speed (V): The speed during steady-level cruise. Higher speeds can increase range if efficiency is maintained.
  • TSFC: Lower TSFC improves range because less fuel is needed per unit of thrust.
  • Lift-to-Drag Ratio (L/D): Represents aerodynamic efficiency. Higher L/D means less thrust is needed to overcome drag.
  • Weight Ratio (ln(W_initial / W_final)): Accounts for fuel burn during flight. As fuel is consumed, the aircraft gets lighter, improving efficiency.

4. Fuel Weight Impact

Fuel weight directly influences range. The logarithmic term shows that carrying more fuel gives diminishing returns:

\ln \frac{W_{initial}}{W_{final}}

  • Large increases in fuel weight lead to smaller incremental range gains.
  • Aircraft design must balance fuel capacity with structural limits and payload.

5. Effect of Efficiency

Range improves with:

  • Higher propulsive efficiency (lower TSFC).
  • Higher thermal efficiency of the engine cycle.
  • Higher aerodynamic efficiency (L/D).

Improving any of these factors leads to better fuel economy and greater range.

6. Range for Propeller-Driven Aircraft

For completeness, the Breguet range equation for propeller aircraft is:

R = \frac{\eta_{prop} c}{c_f} \frac{L}{D} \ln \frac{W_{initial}}{W_{final}}

Where:

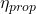  • \eta_{prop} = propeller efficiency
  • c_f = specific fuel consumption (kg/W·s)

Although turboprops use gas turbines, they follow this form because they deliver power through a shaft to the propeller.

7. Design Trade-Offs

Maximizing range requires balancing:

  • Fuel capacity: More fuel means greater weight and possibly lower L/D.
  • Engine efficiency: Advanced cycles and materials improve thermal efficiency.
  • Aerodynamics: High aspect-ratio wings improve L/D but increase weight and structural complexity.
  • Cruise speed: Higher speeds reduce flight time but may increase drag and fuel consumption.

8. Practical Example

Suppose a jet aircraft cruises at 250 m/s, with:

  • TSFC = 0.6 kg/N·h
  • L/D = 15
  • Weight ratio = 1.3 (W_initial / W_final)

Convert TSFC to consistent units and apply:

R \propto V \times \frac{L}{D} \times \ln \frac{W_{initial}}{W_{final}}

Range can be improved by:

  • Reducing TSFC through better engines.
  • Increasing L/D through aerodynamic design.
  • Optimizing weight management.

9. Importance in Aircraft Operations

Range determines:

  • Mission capability (e.g., long-haul vs short-haul)
  • Fuel planning
  • Airline route economics
  • Military reach and refueling needs

Engineers design propulsion systems not just for raw thrust, but for optimal range within operational constraints.

10. Summary

Range analysis links engine performance, fuel efficiency, and aerodynamic design. By understanding how thrust-specific fuel consumption, lift-to-drag ratio, and fuel weight affect range, engineers can design aircraft to meet mission profiles efficiently and sustainably.

Shopping Cart
Scroll to Top