Standard Atmosphere

By /

The standard atmosphere is a reference model that defines how atmospheric properties change with altitude. It provides engineers and pilots with a consistent basis for calculations in aerodynamics, flight mechanics, and aircraft performance.

1. Purpose of the Standard Atmosphere

  • Provides a uniform set of atmospheric conditions for design and testing.
  • Essential for performance calculations (lift, drag, engine thrust).
  • Enables comparison of aircraft performance across different locations and times.

2. Properties Defined

The standard atmosphere defines variations of:

  • Pressure (P)
  • Temperature (T)
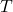  • Density (\rho)
  • Speed of sound (a)

as functions of geopotential altitude.

3. International Standard Atmosphere (ISA)

The most widely used model is the International Standard Atmosphere (ISA).

3.1 Sea-Level Standard Conditions

  • Temperature: T_0 = 288.15 \text{ K} \ (15^\circ \text{C})
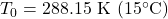
  • Pressure: P_0 = 101325 \ \text{Pa}
  • Density: \rho_0 = 1.225 \ \text{kg/m}^3
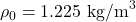
  • Speed of sound: a_0 \approx 340.3 \ \text{m/s}

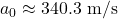
3.2 Lapse Rate

  • Lapse rate: The rate at which temperature decreases with altitude.

For the troposphere (up to 11 km):

\frac{dT}{dh} = -6.5 \ \text{K/km}

Above 11 km (stratosphere), temperature is constant or increases in layers.

4. ISA Temperature Equation

For altitudes within the troposphere (up to 11 km):

T = T_0 + L h

Where:

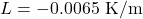  • L = -0.0065 \ \text{K/m} (lapse rate)
  • h = Geopotential altitude (m)

5. ISA Pressure Equation

For altitudes within the troposphere:

P = P_0 \left( \frac{T}{T_0} \right)^{\frac{-g}{LR}}

Where:

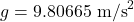  • g = 9.80665 \ \text{m/s}^2 (standard gravity)
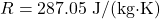  • R = 287.05 \ \text{J/(kg·K)} (specific gas constant for air)

6. ISA Density Equation

Density is obtained from the ideal gas law:

\rho = \frac{P}{R T}

7. Speed of Sound

Speed of sound varies with temperature:

a = \sqrt{\gamma R T}

Where:

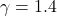  • \gamma = 1.4 (ratio of specific heats for air)

8. Layers of the Standard Atmosphere

  • Troposphere (0–11 km): Temperature decreases linearly.
  • Tropopause (≈11 km): Isothermal layer.
  • Stratosphere (≈11–50 km): Temperature rises in steps.

Each layer has its own lapse rate or isothermal behavior.

9. Applications in Flight Mechanics

  • Performance charts assume standard atmosphere conditions.
  • Airspeed calibrations (true, calibrated, indicated).
  • Engine performance predictions.
  • Altimeter settings and altitude readings.

10. Summary

The standard atmosphere model offers a consistent, idealized description of Earth’s atmosphere for engineering analysis. By defining temperature, pressure, density, and speed of sound variations with altitude, it enables standardized calculations crucial to aircraft design, performance prediction, and flight operations.

Shopping Cart
Scroll to Top