Statically Determinate Trusses

By /

1. Introduction to Trusses

A truss is a structure composed of straight slender members joined at their ends, typically arranged in triangular units to carry loads efficiently. In aerospace engineering, trusses are often used in frameworks like landing gear, space frames, and old aircraft fuselages due to their high strength-to-weight ratio.

2. Assumptions in Truss Analysis

For ideal truss analysis:

  • All loads and reactions act only at joints.
  • Members are connected by frictionless pins.
  • Each member is a two-force member (only axial tension or compression).
  • Self-weight of members is negligible unless specified.

3. Classification of Trusses

3.1 Planar Trusses

  • Members lie in a single plane.
  • Used for 2D load-carrying structures (e.g., bridges, simple aerospace frames).

3.2 Space Trusses

  • Members extend in three dimensions.
  • Suitable for 3D frameworks in aerospace and satellite structures.

4. Determinacy of a Truss

A truss is statically determinate if the internal forces and support reactions can be found using only the equations of static equilibrium.

Determinacy Condition for Planar Trusses:

m + r = 2j
Where:

  • m = number of members
  • r = number of reaction forces
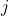  • j = number of joints
  • If 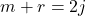m + r = 2j → Statically determinate
  • If 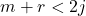m + r < 2j → Mechanism (unstable)
  • If 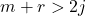m + r > 2j → Statically indeterminate

5. Methods of Truss Analysis

5.1 Method of Joints

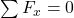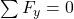  • Uses \sum F_x = 0 and \sum F_y = 0 at each joint.
  • Start from joints where only two unknown member forces exist.

5.2 Method of Sections

  • A “cut” is made through the truss to expose internal forces in selected members.
  • Apply 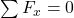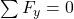\sum F_x = 0, \sum F_y = 0, and \sum M = 0 on one side of the section.

6. Common Truss Configurations

  • Pratt Truss: Diagonals under tension.
  • Howe Truss: Diagonals under compression.
  • Warren Truss: Equilateral triangles, alternating tension/compression.

Each type offers different advantages based on loading type and material usage.

7. Tension and Compression in Members

  • Positive internal force = Tension (pulling).
  • Negative internal force = Compression (pushing).

Accurate member force determination is essential to avoid buckling or failure in compression members, and yielding in tension members.

8. Applications in Aerospace Engineering

  • Aircraft internal frameworks.
  • Launch vehicle support structures.
  • Satellite deployable booms and solar array supports.
Shopping Cart
Scroll to Top