Potential flow theory is an idealized approach in fluid mechanics where the flow is assumed to be inviscid (no viscosity) and irrotational (no vorticity). Under these conditions, the flow velocity field can be derived from a scalar potential function.
This theory provides valuable, simplified solutions for many aerodynamic problems, especially external flows around airfoils, cylinders, and streamlined bodies.
We begin with the simplest case: uniform flow.
1️⃣ What is Uniform Flow?
Uniform flow is the simplest potential flow case where the velocity is constant in magnitude and direction throughout the entire flow field.
Mathematically:
- The velocity vector
has constant components. - There are no spatial variations in speed or direction.
Example: Air flowing steadily past a flat plate aligned with the flow direction.
2️⃣ Mathematical Representation
In 2D Cartesian coordinates (x, y), suppose the flow is purely in the x-direction:
Where:
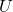= constant velocity magnitude in the x-direction
= unit vector in the x-direction
There are no variations in the y-direction:
Velocity components:
(constant)
3️⃣ Stream Function for Uniform Flow
In potential flow, the stream function 
describes streamlines of the flow.
For uniform flow in x-direction:
Explanation:
- Lines of constant are straight, horizontal lines (parallel to x-axis).
- These are the streamlines of the uniform flow.
4️⃣ Velocity Potential Function
The velocity potential 
is another scalar function describing potential flow:
Explanation:
- Surfaces (or lines) of constant are vertical lines parallel to the y-axis.
- These are equipotential lines, orthogonal to streamlines.
5️⃣ Flow Field Visualization
Key geometric interpretation:
- Streamlines: lines along which fluid particles move. In uniform flow, these are straight, parallel lines in the direction of U.
- Equipotential lines: lines of constant potential, perpendicular to streamlines.
In a diagram:
- Streamlines are horizontal lines.
- Equipotential lines are vertical lines.
This grid of perpendicular lines is the simplest flow net.
6️⃣ Physical Meaning and Applications
Uniform flow models a simple case of free-stream conditions:
✅ Far upstream of an object where flow is undisturbed.
✅ Approximates wind-tunnel inlet conditions.
✅ Forms a building block in superposition to construct more complex flows (e.g. flow past a cylinder).
By understanding uniform flow, we set the foundation for analyzing superposed potential flows like sources, sinks, doublets, and vortices in potential flow theory.
In summary, uniform flow is the simplest potential flow solution. It represents a steady, unchanging flow field with parallel streamlines, constant speed, and linear potential and stream functions. It serves as the fundamental starting point for building more realistic aerodynamic flow models.
