Vortex Flow

By /

In potential flow theory, a vortex represents a flow pattern in which fluid moves in circles around a central point. Unlike sources, sinks, or doublets that add or remove fluid or simulate solid bodies, a vortex imparts rotation to the flow field.

Vortex flow is a key element in modeling real aerodynamic phenomena such as circulation around airfoils and trailing vortices from wings.

1️⃣ Physical Concept

A vortex is a region where fluid circulates around an axis:

✅ Free vortex (ideal): Flow with no rotation of individual fluid particles, even though they move in circles (irrotational outside the core).
✅ Forced vortex (real): Fluid rotates like a solid body with non-zero vorticity.

In potential flow theory, we focus on the free vortex, which is irrotational everywhere except possibly at the center.

2️⃣ Velocity Field in Polar Coordinates

For a point vortex at the origin in 2D polar coordinates (r, θ):

✅ Radial component:

V_r = 0

✅ Tangential component:

V_\theta = \frac{\Gamma}{2\pi r}

Where:

  • \Gamma = circulation strength (m²/s).
    • Positive for counterclockwise rotation.
    • Negative for clockwise rotation.
  • r = radial distance from the center.

Key properties:

  • Velocity decreases with distance (1/r).
  • Flow is purely tangential—particles circle the center.

3️⃣ Circulation

The circulation \Gamma is defined as the line integral of velocity around a closed path enclosing the vortex:

\Gamma = \oint \mathbf{V} \cdot d\mathbf{s}

For the ideal vortex:

\Gamma = 2\pi r V_\theta = \text{constant}

Meaning:

  • Every loop around the vortex encloses the same circulation.
  • This defines the vortex’s strength.

4️⃣ Velocity Potential Function

For a vortex at the origin:

\phi(r, \theta) = -\frac{\Gamma}{2\pi} \theta

Properties:

  • Potential varies linearly with angle θ.
  • Discontinuous across branch cuts (reflecting the multi-valued nature of angle).

5️⃣ Stream Function

\psi(r, \theta) = \frac{\Gamma}{2\pi} \ln r

Properties:

  • Lines of constant ψ are circles around the origin.
  • The streamlines are concentric circles.
  • Each circle represents a path a fluid particle follows.

6️⃣ Flow Field Visualization

✅ Streamlines: Concentric circles around the vortex center.
✅ Equipotential lines: Radial lines outward from the center (perpendicular to streamlines).

Interpretation:

  • Fluid particles move in circles at speeds inversely proportional to distance from the center.
  • At large r, velocity becomes small.
  • Near the center, ideal theory predicts infinite speed (unphysical singularity).

7️⃣ Superposition with Uniform Flow

A crucial application in aerodynamics is adding a vortex to uniform flow:

Uniform flow:

\phi_{uniform} = U r \cos \theta

Vortex:

\phi_{vortex} = -\frac{\Gamma}{2\pi} \theta

Combined potential:

\phi_{total} = U r \cos \theta - \frac{\Gamma}{2\pi} \theta

Stream function:

\psi_{total} = U r \sin \theta + \frac{\Gamma}{2\pi} \ln r

Result:

  • Flow around a cylinder with circulation.
  • Models lifting flows (e.g., airfoils).
  • Explains how circulation creates asymmetric pressure distribution and lift.

8️⃣ Aerodynamic Interpretation: Lift Generation

Kutta–Joukowski Theorem:

L' = \rho U \Gamma

Where:

  • L' = lift per unit span.
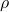  • \rho = fluid density.
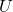  • U = freestream velocity.
  • \Gamma = circulation.

Meaning:

  • Circulation around an airfoil generates lift.
  • The vortex model represents the bound circulation required for lift.

9️⃣ Applications in Aerodynamics

✅ Airfoil theory: Explains lift using circulation.
✅ Trailing vortices: Shed from wingtips due to lift.
✅ Wingtip vortices: Important in wake turbulence modeling.
✅ Vortex sheets and filaments: Advanced modeling of 3D flows.

1️⃣0️⃣ Limitations

❌ Inviscid assumption ignores viscous effects (real vortices have cores).
❌ Infinite velocity at center is unphysical.
❌ No modeling of vortex diffusion or decay.

In real fluids, vortex cores have finite size and rotational flow inside.

In summary, vortex flow is a fundamental potential flow element representing rotational motion around a point. By combining vortices with other elementary flows, aerodynamicists model lift, trailing vortices, and complex circulation patterns critical to aircraft design.

Shopping Cart
Scroll to Top