Vertical Maneuvers

By /

Vertical maneuvers involve flight paths where the aircraft changes altitude significantly, such as loops, pull-ups, push-overs, or zoom climbs. Unlike steady level flight or flat turns, these maneuvers involve accelerations in the vertical plane and result in changing load factors (n), airspeeds, and flight path angles.

Vertical maneuvers are critical in aerobatics, military operations, and flight testing. They help define structural requirements, pilot limits (g-tolerance), and aircraft performance capabilities.

1. Concept of Load Factor in Vertical Flight

Load factor (n) in vertical maneuvers is defined as:

n = \frac{L}{W}

  • n = 1 in steady, level flight.
  • n > 1 in pull-up (positive g’s).
  • n < 1 in push-over (negative g’s).

Load factor represents the apparent weight experienced by the pilot and structure during maneuvering.

2. Types of Vertical Maneuvers

2.1 Pull-up

  • Aircraft transitions from level flight into a climb.
  • Pilot pulls back on the stick.
  • Positive load factor is generated.
  • Used in climb initiation, obstacle clearance, aerobatics.

2.2 Push-over

  • Aircraft transitions from climb to descent.
  • Pilot pushes forward on the stick.
  • Negative load factor is generated.
  • Used for dive entry or inverted maneuvers.

2.3 Loop

  • Complete 360° vertical circle.
  • Constant or variable load factor throughout the maneuver.
  • Requires energy management (airspeed and altitude exchange).

2.4 Zoom Climb

  • Exchange of kinetic energy (speed) for potential energy (altitude).
  • Steep climb initiated at high speed.
  • Limited by available thrust and aerodynamic drag.

3. Force Analysis in Vertical Maneuvers

In vertical flight, forces must balance both weight and required centripetal force for curved flight paths.

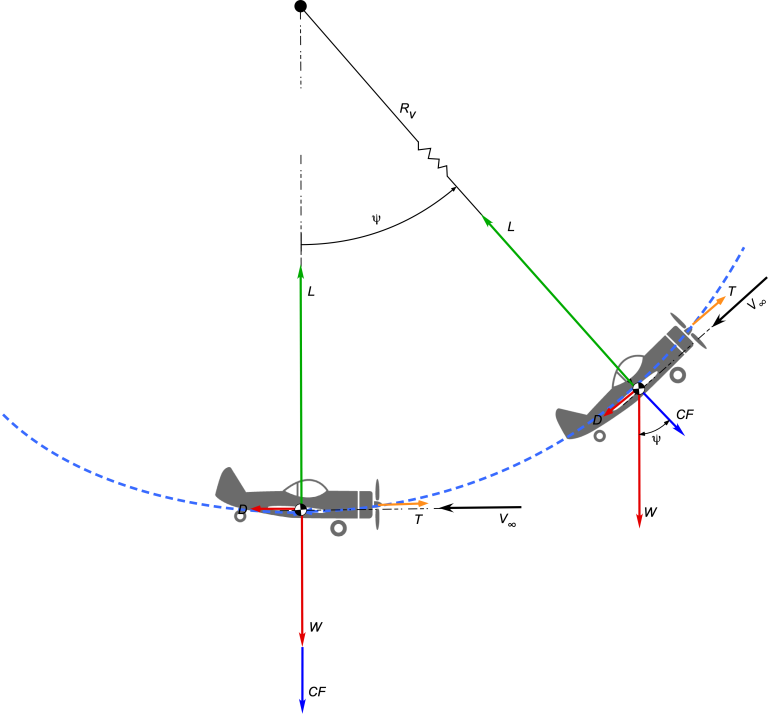
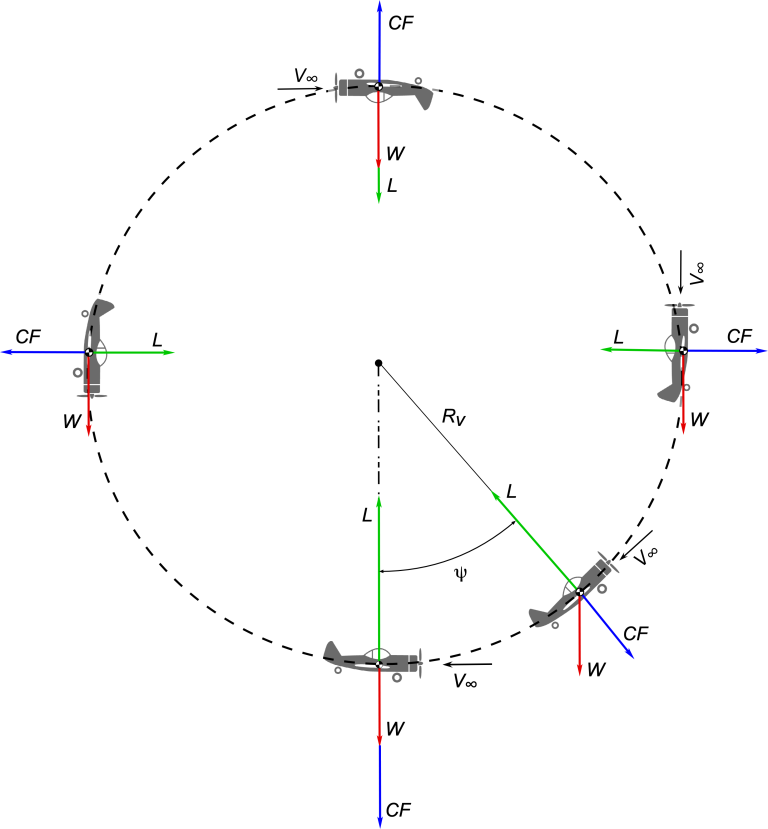
3.1 Circular Vertical Maneuver (Loop Segment)

For a segment of vertical circular motion (e.g., loop or pull-out from a dive):

\sum F = m \frac{V^2}{r}

At the bottom of a loop (pull-up):

L - W = m \frac{V^2}{r}

Load factor:

n = \frac{L}{W} = 1 + \frac{V^2}{g r}

  • Higher speed or tighter radius → higher load factor.
  • Structural limits can be exceeded in aggressive maneuvers.

At the top of a loop (inverted):

L + W = m \frac{V^2}{r}

Load factor:

n = -1 + \frac{V^2}{g r}

  • Negative g’s (inverted flight) challenge both structure and pilot tolerance.

4. Energy Considerations

Vertical maneuvers involve exchange between kinetic energy (KE) and potential energy (PE):

KE + PE = \text{constant (neglecting drag)}

  • Climbing → KE decreases, PE increases.
  • Diving → KE increases, PE decreases.
  • Real flight: Drag and thrust must be considered.

Example: A zoom climb trades initial high speed for altitude. The maximum altitude is limited by initial energy and aerodynamic drag.

5. Structural and Operational Limits

Aircraft design includes structural limits for:

  • Positive limit load factor: e.g., +2.5g (transport), +6g (aerobatic).
  • Negative limit load factor: e.g., –1.0g (transport), –3g (aerobatic).

Vertical maneuvers must be planned to stay within these load factor limits to avoid permanent structural damage or failure.

6. Pilot Physiological Limits

  • Positive g’s: Blood pools in legs → risk of greyout or blackout.
  • Typical pilot limit without G-suit: +4g to +5g sustained.
  • Negative g’s: Blood rushes to head → redout, disorientation.
  • Negative g-tolerance is typically lower (–2g to –3g).

Proper training and equipment (G-suits, straining maneuvers) help manage high-g vertical maneuvers.

7. Stall Considerations in Vertical Maneuvers

Load factor affects stall speed:

V_{stall, n} = V_{stall} \sqrt{n}

  • High-g pull-ups increase stall speed significantly.
  • Maneuvering speed (Va) ensures that full control deflection at or below Va will stall the aircraft before exceeding structural limits.

Pilots must manage speed carefully during vertical maneuvers to avoid accelerated stalls.

8. Examples of Vertical Maneuver Equations

✅ Load Factor in Pull-up:

n = 1 + \frac{V^2}{g r}

✅ Load Factor in Push-over:

n = 1 - \frac{V^2}{g r}

✅ Stall Speed at Load Factor n:

V_{stall,n} = V_{stall} \sqrt{n}

✅ Energy Conservation:

\frac{1}{2} m V^2 + m g h = \text{constant}

9. Operational Implications

  • High-speed pull-outs from dives can easily exceed limit load factors.
  • Loops require careful entry speed planning to avoid stalls at the top and excessive G at the bottom.
  • Zoom climbs can achieve high altitudes quickly but require excess thrust and careful speed management.
  • Maneuvering speed (Va) sets a safe operational limit for abrupt control inputs.

10. Summary

Vertical maneuvers are an essential part of aircraft flight, used in climbing, diving, aerobatics, and combat tactics. They:

  • Generate varying load factors that stress the airframe.
  • Require management of speed, bank angle, and energy.
  • Are constrained by aerodynamic stall, structural limits, and pilot g-tolerance.

Understanding the physics of vertical maneuvers ensures safe, efficient, and precise aircraft handling in all flight regimes.

Shopping Cart
Scroll to Top