For bodies moving in elliptical orbits under the influence of an inverse-square central force, such as gravity, the orbital period depends on the size of the ellipse but not on its shape (eccentricity).
Kepler’s Third Law for Ellipses
Johannes Kepler discovered empirically that for planets orbiting the Sun, the square of the orbital period 
is proportional to the cube of the semi-major axis 
of the ellipse:
Newton showed that this relationship follows directly from universal gravitation. For any elliptical orbit around a central mass 
, the period is given by:
where:
- is the semi-major axis of the ellipse,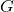
is the gravitational constant,- is the mass of the central body.
Derivation Outline
Although the exact derivation involves integrating over the orbital motion, the key idea is that conservation of energy and angular momentum in an inverse-square field leads to:
which relates total mechanical energy to . By applying conservation laws and solving for the time to sweep the entire ellipse, one arrives at the period formula above.
Key Features
- The period depends only on the semi-major axis , not on the eccentricity
. - All ellipses with the same around the same central mass have the same period.
- For a circular orbit,
, recovering:
Physical Interpretation
- Larger orbits (larger ) have longer periods.
- Bodies move faster near periapsis and slower near apoapsis, but the total time to complete an orbit depends only on .
Examples
- Earth’s orbit around the Sun:
gives 
.
Satellites in highly elliptical transfer orbits have periods determined solely by their semi-major axis, regardless of how stretched the ellipse is.
Kepler’s Third Law thus provides a powerful and simple tool for predicting orbital periods of planets, satellites, and spacecraft in elliptical orbits.
