Beams with Overhangs and Combined Loadings

By /

1. Introduction

In real-world structural systems, beams are often not limited to simple supports between two points—they may extend beyond supports, forming overhangs. Additionally, these beams are subjected to multiple types of loads simultaneously, such as point loads, uniformly distributed loads (UDLs), and moments. Such systems are called beams with combined loading.

Analyzing such beams requires a solid understanding of support reactions, shear force and bending moment equations, and superposition of load effects.

2. Overhanging Beams

A beam with overhang extends beyond one or both of its supports. Overhangs are common in aircraft wing spars, canopies, balconies, and more.

2.1 Types of Overhangs

  • Single Overhang: Beam extends beyond one support.
  • Double Overhang: Beam extends beyond both supports.

These extensions experience bending moments and shear forces and must be carefully analyzed to avoid failure.

3. Combined Loadings

In aerospace structures, beams often experience more than one type of load simultaneously, e.g.:

  • A point load due to engine thrust mounts
  • A UDL due to fuel tanks or distributed wing lift
  • A couple moment from maneuver loads

To analyze combined loading:

  • Break into components
  • Analyze each load separately
  • Apply superposition principle (since the system is linear and elastic)

4. Example: Overhanging Beam with UDL and Point Load

Problem Statement

A simply supported beam of length L = 8, \text{m} has an overhang of 2, \text{m} beyond support B. A UDL of w = 5, \text{kN/m} acts over the entire span AB (0 \le x \le 8, \text{m}) and a point load of P = 10, \text{kN} acts at the free end C (x = 10, \text{m}).

Support Reactions

Let supports be at A (x = 0) and B (x = 8).

  • Total UDL = wL = 5 \times 8 = 40, \text{kN}
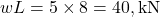
  • Its centroid = 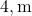4, \text{m} from A
  • The point load of 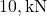10, \text{kN} at x = 10, \text{m}

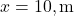
Taking moments about A:

\sum M_A = 0 = -40 \times 4 - 10 \times 10 + R_B \times 8 \ \Rightarrow R_B = \frac{160 + 100}{8} = 32.5, \text{kN}

Then, vertical equilibrium:

R_A + R_B = 40 + 10 = 50, \text{kN} \ \Rightarrow R_A = 50 - 32.5 = 17.5, \text{kN}

Shear Force Calculation

Break the beam into segments:

  • Segment AB (0 ≤ x ≤ 8):

V(x) = R_A - w x

Segment BC (8 ≤ x ≤ 10):

V(x) = R_A - w \cdot 8 - P = 17.5 - 40 - 10 = -32.5, \text{kN}

Bending Moment Calculation

For 0 \le x \le 8:

M(x) = R_A x - \frac{w x^2}{2} = 17.5x - \frac{5x^2}{2}

Maximum bending moment occurs where \frac{dM}{dx} = 0:

\frac{dM}{dx} = 17.5 - 5x = 0 \Rightarrow x = 3.5, \text{m}

Substitute into M(x):

M_{\text{max}} = 17.5 \cdot 3.5 - \frac{5 \cdot (3.5)^2}{2} = 61.25 - 30.625 = 30.625, \text{kNm}

For 8 < x \le 10 (overhang):

At x = 10:

M(10) = R_A \cdot 10 - w \cdot \frac{(10)^2}{2} - P \cdot (10 - 10) = 175 - 250 = -75, \text{kNm}

5. Superposition of Load Effects

If a beam is subjected to both a UDL and a point moment, or multiple loads, compute internal forces due to each individually, then add results algebraically:

M_{\text{total}}(x) = M_1(x) + M_2(x) + \dots

V_{\text{total}}(x) = V_1(x) + V_2(x) + \dots

6. Additional Example: Beam with UDL + Moment

A cantilever beam of length L = 3, \text{m} has:

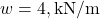  • UDL w = 4, \text{kN/m} over entire length
  • Clockwise moment 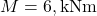M = 6, \text{kNm} applied at free end

Shear Force:

V(x) = -w (L - x) = -4 (3 - x)

Bending Moment:

M(x) = -M + \frac{w (L - x)^2}{2} = -6 + \frac{4 (3 - x)^2}{2}

7. Summary and Key Points

  • Overhanging beams have extended segments beyond supports and often carry additional loads.
  • Combined loading requires analyzing effects separately and summing.
  • Reaction calculation and moment equations rely on equilibrium and calculus.
  • Use segment-wise equations for accurate internal force distribution.
Shopping Cart
Scroll to Top