Compatibility Conditions in Indeterminate Structures

By /

1. Introduction

In structural analysis, especially for statically indeterminate structures, equilibrium equations alone are insufficient to find all unknown reactions and internal forces. Therefore, we must incorporate compatibility conditions — mathematical expressions ensuring that the deformed shape of the structure satisfies physical continuity and boundary constraints.

Compatibility ensures that members:

  • Fit together without gaps or overlaps,
  • Deform in a manner consistent with connectivity,
  • Satisfy displacement boundary conditions (zero deflection at fixed supports, same displacement at connected joints, etc.)

2. Why Compatibility is Needed

Let’s contrast:

  • Statically Determinate Structure:
    All support reactions and member forces can be found using only equilibrium:

\sum F_x = 0, \quad \sum F_y = 0, \quad \sum M = 0

Statically Indeterminate Structure:
The number of unknowns exceeds available equilibrium equations. The extra equations needed come from compatibility of displacements.

Without compatibility, we may get mathematically valid results that are physically impossible — like disconnected or overlapping joints.

3. Types of Compatibility Conditions

3.1 Geometric Compatibility

These arise from:

  • Displacement continuity at joints
  • Rotational continuity at hinges/supports
  • Known fixed displacements (e.g., zero displacement at a fixed support)

3.2 Material and Structural Compatibility

When deformation is governed by elastic behavior (Hooke’s law), compatibility links applied loads to displacements via:

  • Axial deformation:

\delta = \frac{PL}{AE}

Bending deformation:
\delta = \frac{PL^3}{3EI}, \quad \theta = \frac{PL^2}{2EI}
(depending on boundary conditions and load type)

4. Steps to Apply Compatibility

For 1 degree of indeterminacy (DOI = 1):

  1. Remove one redundant force to create a primary (determinate) structure.
  2. Apply unit value of the redundant force and calculate displacement at its point of action (call it \Delta_r ).
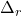  3. Calculate displacement due to actual loading on the primary structure at the same location (call it \Delta_0 ).
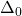  4. Apply compatibility condition: \Delta_0 + R \Delta_r = 0 where R is the unknown redundant force.

For higher degrees of indeterminacy, repeat for each redundant and solve the resulting system of equations.

5. Example – Axially Loaded Bar

Structure:
Two rods (AB and BC) of lengths L_1 and L_2 , made of different materials, are joined end to end and held between two rigid supports. A force P is applied at the joint.

Unknown: Internal forces in AB and BC.

Compatibility:
Since the supports are rigid, total elongation = 0: \delta_{AB} + \delta_{BC} = 0

Using \delta = \frac{PL}{AE} for each: \frac{P_1 L_1}{A_1 E_1} + \frac{P_2 L_2}{A_2 E_2} = 0

Combined with P_1 + P_2 = P , we can solve for P_1 and P_2 .

6. Example – Propped Cantilever Beam

Problem:
A cantilever beam of length L is fixed at one end and simply supported at the other (a propped cantilever), with a central point load P .

Degree of Indeterminacy = 1 (extra reaction at the prop)

Solution:

  1. Treat support reaction at the prop as redundant R
  2. Remove prop → simple cantilever → compute deflection 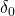\delta_0 at the prop location
  3. Apply unit load at prop → compute flexibility coefficient \delta_R
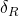
  4. Apply compatibility:\delta_0 + R \delta_R = 0 \quad \Rightarrow \quad R = -\frac{\delta_0}{\delta_R}

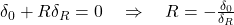
7. Common Compatibility Scenarios

ScenarioCompatibility Condition
Two rods between walls \delta_1 + \delta_2 = 0
Beam with extra supportDeflection at extra support = 0
Frame with multiple supportsHorizontal or vertical displacements at joints must be equal (based on geometry)
Hinged connectionsSlope of members must match at hinge

8. Compatibility in Trusses

In trusses, compatibility ensures:

  • Equal displacement at common joints
  • No member elongates or contracts inconsistently

Example:
For a redundant truss member, total change in length = deformation due to external loads + deformation due to redundant = 0.

9. Compatibility in Aerospace Applications

Aircraft structures are often highly redundant (multi-longeron fuselages, wing-boxes, etc.). Ensuring compatibility:

  • Prevents overstressing components
  • Accurately predicts load paths
  • Accounts for elastic interactions in complex assemblies (e.g., skin-stringer panels)

10. Summary

  • Compatibility conditions are essential in solving statically indeterminate problems.
  • They are based on geometry and material behavior.
  • Used in combination with equilibrium equations and constitutive laws to determine all unknowns.
Shopping Cart
Scroll to Top