Concept of Escape Velocity

By /

Escape velocity is the minimum speed an object must have to break free from the gravitational attraction of a massive body without further propulsion. It represents the threshold at which the object’s total mechanical energy becomes zero, allowing it to move to infinite distance with zero residual speed.

Physical Meaning

When an object is launched upward against gravity, it loses kinetic energy while gaining gravitational potential energy. To escape completely, its initial kinetic energy must be enough to offset the entire gravitational potential well:

  • If it has less than escape velocity, it will eventually stop and fall back.
  • If it has exactly escape velocity, it will slow to zero speed at infinity.
  • If it has more than escape velocity, it will continue moving away indefinitely with leftover speed.

Derivation of Escape Velocity

Consider an object of mass m at the surface of a spherical planet of mass M and radius R. The gravitational potential energy at distance r is:

U(r) = -\frac{G M m}{r}

At the planet’s surface:

U(R) = -\frac{G M m}{R}

The kinetic energy is:

K = \frac{1}{2} m v^2

To just escape to infinity (where U = 0 and v = 0), total energy at launch must be zero:

E = K + U = 0

Thus:

\frac{1}{2} m v_{\text{esc}}^2 - \frac{G M m}{R} = 0

Solving for v_{\text{esc}}:

v_{\text{esc}} = \sqrt{\frac{2 G M}{R}}

Key Features

  • Independent of mass m: Escape velocity depends only on the central body’s mass M and radius R, not on the escaping object’s mass.
  • Depends on distance: If launching from altitude h above the surface, replace R with R + h:

v_{\text{esc}} = \sqrt{\frac{2 G M}{R + h}}

Decreases with altitude: The higher you start, the lower the escape velocity.

Example Values

  • Earth: M \approx 5.972 \times 10^{24} , \text{kg}, R \approx 6.371 \times 10^6 , \text{m}. v_{\text{esc}} \approx 11.2 , \text{km/s}.
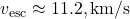  • Moon: v_{\text{esc}} \approx 2.4 , \text{km/s}.
  • Jupiter: v_{\text{esc}} \approx 59.5 , \text{km/s}.

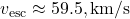Relation to Orbital Motion

Escape velocity is linked to circular orbital speed v_{\text{orb}}:

v_{\text{esc}} = \sqrt{2} , v_{\text{orb}}

where:

v_{\text{orb}} = \sqrt{\frac{G M}{R}}

This relation highlights that to escape, an object needs roughly 41% more speed than to remain in low circular orbit.

Energy Perspective

For escape:

E = 0

Below escape velocity:

E < 0 (bound orbit).

Above escape velocity:

E > 0 (unbound hyperbolic trajectory).

Importance in Space Dynamics

Escape velocity is critical for:

  • Launching interplanetary missions.
  • Designing rockets with sufficient propulsion.
  • Understanding how bodies can retain or lose atmospheres over time.

It defines a fundamental threshold for transitioning from bound to unbound motion in gravitational fields, essential in astrodynamics and planetary science.

Shopping Cart
Scroll to Top