Conservation Laws in Central Force Motion

By /

Central force motion possesses important conservation laws that simplify the analysis of particle trajectories. These laws arise due to the symmetry and nature of central forces, which depend only on distance from the center.

Conservation of Angular Momentum

A key property of central forces is that they exert no torque about the center of force. The torque \boldsymbol{\tau} with respect to the center is:

\boldsymbol{\tau} = \mathbf{r} \times \mathbf{F}

For a central force:

\mathbf{F} = F(r) , \hat{\mathbf{r}}

This means:

\mathbf{r} \times \mathbf{F} = r , \hat{\mathbf{r}} \times F(r) , \hat{\mathbf{r}} = 0

Therefore, torque is zero:

\boldsymbol{\tau} = 0

Since torque is the time derivative of angular momentum \mathbf{L}:

\frac{d\mathbf{L}}{dt} = \boldsymbol{\tau} = 0

Angular momentum is conserved:

\mathbf{L} = \mathbf{r} \times \mathbf{p} = \text{constant}

where \mathbf{p} = m \mathbf{v} is the linear momentum.

Areal Velocity

Conservation of angular momentum implies conservation of areal velocity:

\frac{dA}{dt} = \frac{1}{2} r^2 \frac{d\theta}{dt} = \text{constant}

This is the basis for Kepler’s Second Law: equal areas in equal times.

Conservation of Energy

If the central force is conservative, it has an associated potential energy function V(r):

\mathbf{F} = -\nabla V(r) = -\frac{dV}{dr} , \hat{\mathbf{r}}

Total mechanical energy E is conserved:

E = T + V(r) = \text{constant}

where:

  • Kinetic energy T = \frac{1}{2} m v^2.
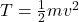  • Potential energy 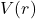V(r) depends only on r.

This conservation allows determination of allowed regions of motion (turning points) and the shape of trajectories.

Implications of Conservation Laws

  • Angular momentum conservation confines motion to a plane.
  • Energy conservation defines the class of orbits (bound or unbound).
  • Combined, these laws lead to the derivation of conic-section trajectories (circles, ellipses, parabolas, hyperbolas).

These conservation principles are foundational tools in analyzing orbital mechanics and predicting satellite or planetary paths.

Shopping Cart
Scroll to Top