Definition of Central Force

By /

A central force is a force that is always directed along the line joining a particle to a fixed point (called the center) and whose magnitude depends only on the distance between them.

This fixed point is often called the center of force or force center. Central forces are important in space dynamics because gravitational forces between two bodies are central in nature.

Mathematical Definition

Mathematically, a central force F acting on a particle of mass m at position vector r relative to the center is expressed as:

\mathbf{F} = F(r) , \hat{\mathbf{r}}

where:

  • F(r) is a scalar function depending only on the radial distance r = |\mathbf{r}|.
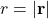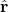  • \hat{\mathbf{r}} is the unit vector in the direction of \mathbf{r}.

This shows that the force always points radially—either toward or away from the center.

Radial Nature of Central Forces

By definition:

\mathbf{F} \cdot \hat{\boldsymbol{\theta}} = 0

where \hat{\boldsymbol{\theta}} is the unit vector perpendicular to \hat{\mathbf{r}}. This indicates there is no tangential component of force; the entire force acts along the radius.

Examples of Central Forces

  1. Gravitational Force between two point masses:

\mathbf{F} = -\frac{G M m}{r^2} , \hat{\mathbf{r}}

where G is the gravitational constant, and M and m are the masses.

Electrostatic Force between two point charges:

\mathbf{F} = \frac{1}{4\pi \varepsilon_0} \frac{q_1 q_2}{r^2} , \hat{\mathbf{r}}

Both forces depend only on r and act along \hat{\mathbf{r}}.

Key Features

  • Magnitude depends only on radial distance r.
  • Direction is along the radius vector.
  • Conservative Nature: Central forces are typically conservative, meaning they can be derived from a potential function V(r):

\mathbf{F} = -\nabla V(r) = -\frac{dV}{dr} , \hat{\mathbf{r}}

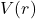Because of these properties, central forces conserve angular momentum and allow analysis of orbital motion in terms of conic sections.

Shopping Cart
Scroll to Top