Gas Properties and Equations of State

By /

Gas properties and equations of state form the essential foundation for analyzing thermodynamic cycles, combustion, and propulsion systems. Understanding how gases behave under varying conditions is crucial for accurate calculations in aircraft engine design and performance analysis.

1. Ideal Gas Law

The ideal gas law is a simple equation of state that relates pressure, volume, temperature, and the amount of gas:

pV = nRT

Where:

  • p = pressure (Pa)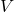
  • V = volume (m³)
  • n = number of moles
  • R = universal gas constant (8.314 J/mol·K)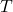
  • T = temperature (K)

For engineering applications involving mass, it is often expressed as:

p = \rho R_s T

Where:

  • \rho = density (kg/m³)
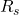  • R_s = specific gas constant (J/kg·K)

R_s = \frac{R}{M}

  • M = molar mass (kg/mol)

For air (approximately 28.97 g/mol):

R_s \approx 287 \text{ J/kg·K}

2. Specific Heats

Specific heat is the amount of heat required to raise the temperature of a unit mass of a substance by one degree.

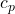  • c_p: specific heat at constant pressure
  • c_v: specific heat at constant volume

For ideal gases:

c_p - c_v = R_s

Ratio of specific heats (gamma):

\gamma = \frac{c_p}{c_v}

For air at standard conditions:

c_p \approx 1005 \text{ J/kg·K}

c_v \approx 718 \text{ J/kg·K}

\gamma \approx 1.4

Importance:

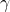  • \gamma affects speed of sound and compressible flow behavior.
  • Needed for isentropic relations in nozzles and compressors.

3. Internal Energy and Enthalpy

For ideal gases, internal energy and enthalpy depend only on temperature:

  • Internal Energy:

u = c_v T

  • Enthalpy:

h = c_p T

Change in internal energy:

\Delta u = c_v \Delta T

Change in enthalpy:

\Delta h = c_p \Delta T

These relations are essential in analyzing combustion (energy release) and turbine/compressor work.

4. Equations of State for Gas Mixtures

Aircraft engines use air–fuel mixtures, which are gas mixtures with varying composition.

For mixtures:

pV = n_{total}RT

  • Dalton’s Law of Partial Pressures:

p_{total} = \sum p_i

Each gas behaves ideally, contributing to the total pressure.

Specific gas constant for mixture:

R_{mix} = \frac{R}{M_{mix}}

Where M_{mix} = mean molar mass of the mixture.

Enthalpy of a mixture:

h_{mix} = \sum y_i h_i

  • y_i = mass or mole fraction
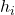  • h_i = specific enthalpy of component i

These relations are used in combustion calculations to determine temperature rise and composition of exhaust gases.

5. Real Gas Behavior

At very high pressures or very low temperatures, gases deviate from ideal behavior.

  • Compressibility factor (Z):

Z = \frac{pV}{nRT}

For ideal gases: Z = 1.

For real gases: Z \neq 1.

Aircraft engines usually operate at conditions where air and combustion gases can be approximated as ideal, but real gas effects may be considered in high-pressure combustion analysis or in cryogenic rocket propellants.

6. Importance in Aircraft Propulsion

Understanding gas properties and equations of state is essential for:

  • Compressor and turbine design (isentropic relations)
  • Nozzle flow analysis (Mach number, expansion)
  • Combustion analysis (fuel-air ratio, exhaust gas composition)
  • Cycle calculations (Brayton cycle efficiency)

Accurate gas property data ensures reliable performance predictions and safe engine operation.

Mastering these fundamentals provides the groundwork for more advanced topics such as compressible flow, combustion thermodynamics, and engine cycle analysis in aircraft propulsion systems.

Shopping Cart
Scroll to Top