General Equation of Orbit

By /

The general equation of orbit describes the path of a particle moving under a central force in a plane. By using the conservation of angular momentum and Newton’s second law in polar coordinates, we can derive a differential equation that determines the orbit shape.

Conservation of Angular Momentum

From conservation of angular momentum per unit mass:

r^2 , \dot{\theta} = h

where h is a constant.

This allows us to write:

\frac{d\theta}{dt} = \frac{h}{r^2}

Change of Variables

To simplify the radial equation, we introduce:

u = \frac{1}{r}

Differentiating with respect to \theta:

\frac{dr}{d\theta} = -\frac{1}{u^2} \frac{du}{d\theta}

Further derivatives yield:

\frac{d^2 r}{d\theta^2} = \frac{2}{u^3} \left(\frac{du}{d\theta}\right)^2 - \frac{1}{u^2} \frac{d^2u}{d\theta^2}

However, a standard and simpler result from the chain rule gives:

\frac{d^2u}{d\theta^2} + u = -\frac{F(r)}{m h^2 u^2}

The General Orbit Differential Equation

The derived form of the orbit equation is:

\frac{d^2u}{d\theta^2} + u = -\frac{F\left(\frac{1}{u}\right)}{m h^2 u^2}

where:

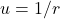  • u = 1/r is the reciprocal of the radius.
  • F(r) is the central force as a function of r.
  • h is the specific angular momentum.

This second-order differential equation governs the shape of the orbit.

Example: Inverse-Square Law

For gravitational attraction:

F(r) = -\frac{G M m}{r^2}

Substituting:

-\frac{F(r)}{m h^2 u^2} = \frac{G M}{h^2}

The orbit equation becomes:

\frac{d^2u}{d\theta^2} + u = \frac{G M}{h^2}

The general solution is:

u(\theta) = \frac{G M}{h^2} \left[ 1 + e \cos(\theta - \theta_0) \right]

where:

  • e is the orbital eccentricity.
  • \theta_0 is the orientation constant.

This solution represents a conic section (circle, ellipse, parabola, or hyperbola), depending on e.

Significance

The general equation of orbit links the nature of the central force to the trajectory’s geometric shape. For any given central force law F(r), solving this differential equation determines the path of the particle in space.

Shopping Cart
Scroll to Top