Mathematical Form of Central Forces

By /

A central force is characterized by its dependence on the radial distance from a fixed point and by its direction being always along the radius vector. The general mathematical expression for a central force acting on a particle at position r is:

\mathbf{F} = F(r) , \hat{\mathbf{r}}

where:

  • F(r) is a scalar function that depends only on the distance r = |\mathbf{r}|.
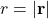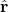  • \hat{\mathbf{r}} is the unit vector pointing from the center toward the particle.

This form ensures that the force has no component perpendicular to \hat{\mathbf{r}}. It acts purely in the radial direction.

Scalar Form

In scalar notation, the magnitude of the force is:

F(r) = \pm \frac{k}{r^n}

where:

  • k is a constant (positive or negative depending on the nature of the force),
  • n is the exponent defining how the force varies with distance.

Examples:

  • Gravitational force: F(r) = -\frac{G M m}{r^2}
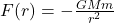
  • Electrostatic force: F(r) = \frac{1}{4\pi \varepsilon_0} \frac{q_1 q_2}{r^2}

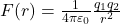
Vector Form in Polar Coordinates

In polar (planar) coordinates (r, \theta), the position vector is:

\mathbf{r} = r , \hat{\mathbf{r}}

The force vector becomes:

\mathbf{F} = F(r) , \hat{\mathbf{r}}

with no \hat{\boldsymbol{\theta}} component:

\mathbf{F} \cdot \hat{\boldsymbol{\theta}} = 0

Conservative Nature and Potential Energy

If the central force is conservative, it can be derived from a potential energy function V(r):

\mathbf{F} = -\nabla V(r) = -\frac{dV}{dr} , \hat{\mathbf{r}}

For inverse-square law forces:

V(r) = -\frac{G M m}{r}

This relationship links force and potential energy, simplifying the analysis of orbital motion.

Summary of Mathematical Properties

  • Direction: Always along \hat{\mathbf{r}}
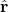
  • Magnitude: Function only of r
  • Conservative: Can be expressed as gradient of a potential
  • Example forms: 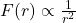F(r) \propto \frac{1}{r^2} (gravitational, electrostatic)
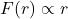    F(r) \propto r (harmonic oscillator)

These properties make central forces fundamental in describing planetary and satellite motion.

Shopping Cart
Scroll to Top