Range & Endurance of Jet Airplane

By /

Range and endurance are critical performance metrics describing how far or how long an aircraft can fly on a given amount of fuel. For jet airplanes, these depend on engine characteristics, aerodynamic efficiency, fuel consumption, and operating conditions. Unlike propeller aircraft, jets derive thrust directly from high-speed exhaust, which influences how range and endurance are calculated.

1. Definitions

1.1 Range

  • Range (R): The maximum horizontal distance an aircraft can travel with a given fuel supply.
  • Important for route planning, minimizing refueling stops, and long-haul operations.

1.2 Endurance

  • Endurance (E): The maximum time an aircraft can stay airborne with a given fuel load.
  • Critical for holding patterns, loiter missions, and fuel management.

2. Jet Engine Fuel Consumption Metric

Unlike propeller aircraft (which use BSFC based on power), jets use Thrust Specific Fuel Consumption (TSFC):

TSFC = \frac{\text{Fuel flow rate}}{\text{Thrust produced}}

Units: lb/(lbf·hr) or kg/(N·hr).

  • Lower TSFC → more efficient engine.

3. Fuel Flow Rate for Jets

Fuel flow rate:

\dot{m}_f = TSFC \times T

Where:

  • \dot{m}_f = Fuel mass flow rate
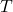  • T = Thrust required

4. Endurance of a Jet Airplane

Endurance (E) is total time airborne:

E = \frac{\text{Total fuel}}{\dot{m}_f}

Substituting fuel flow rate:

E = \frac{W_f}{TSFC \times T}

Where:

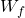  • W_f = Total fuel weight

4.1 Condition for Maximum Endurance

To maximize E:

E \propto \frac{1}{T}

  • Minimize thrust required.

For jet aircraft in level flight:

T = D

So:

E \propto \frac{1}{D}

Key Insight:

  • Minimum drag yields maximum endurance.

5. Range of a Jet Airplane

Range (R) is horizontal distance covered:

R = V \times E

Using fuel flow rate:

R = V \times \frac{W_f}{TSFC \times T}

In level flight (T = D):

R = \frac{V W_f}{TSFC \times D}

5.1 Lift-to-Drag Ratio

Drag can be expressed as:

D = \frac{W}{(L/D)}

Substitute into the range equation:

R = \frac{V W_f (L/D)}{TSFC \times W}

Simplifies to:

R \propto \frac{V}{TSFC} \times \frac{L}{D}

Key Insight:

  • Maximize \frac{V}{TSFC} \times \frac{L}{D} for maximum range.

6. Breguet Range Equation (Jets)

For jets, the classical range formula (assuming constant TSFC, L/D, and speed) is:

R = \frac{V}{TSFC} \times \frac{L}{D} \times \ln \left( \frac{W_i}{W_f} \right)

Where:

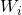  • W_i = Initial weight (start of cruise)
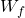  • W_f = Final weight (end of cruise)
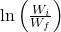  • \ln \left( \frac{W_i}{W_f} \right) = Fuel fraction used during cruise

7. Conditions for Maximum Range

  • High True Airspeed (V): Increases distance per unit time.
  • Low TSFC: More efficient engines.
  • High 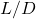L/D Ratio: Aerodynamic efficiency.
  • Optimal Altitude: Balances drag reduction and engine performance.

8. Conditions for Maximum Endurance

  • Minimum Thrust Required (Minimum Drag).
  • Fly at speed that minimizes drag → often slower than max range speed.
  • Used for loiter, holding patterns, or fuel conservation.

9. Comparison: Jet vs. Propeller Aircraft

FeaturePropeller AircraftJet Aircraft
Fuel metricBSFC (per power)TSFC (per thrust)
Max enduranceMinimum power requiredMinimum thrust required
Max range speedBest (V / P_R) or max L/DBest (V / TSFC) × (L/D)
Altitude effectsEngine power loss with altitudeJets often more efficient at altitude

10. Operational Significance

  • Max Range Flight:
    • Long-haul operations.
    • Fuel-efficient cruise planning.
  • Max Endurance Flight:
    • Holding patterns.
    • Loiter (surveillance, military missions).
  • Cruise Altitude Selection:
    • Balances TSFC, 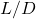L/D, and wind components.

11. Summary

For jet airplanes:

  • Range depends on maximizing \frac{V}{TSFC} \times \frac{L}{D}.
  • Endurance depends on minimizing thrust required (or drag).

Pilots and engineers use these relationships to select optimal speeds and altitudes for missions, plan fuel loads, and ensure efficient, safe flight operations.

Shopping Cart
Scroll to Top