Insights and Tips for GATE Aspirants

Course Image

Structures

Course Progress: 0% (0/48 topics completed)

⏹️ Course Syllabus
Strength of Materials
Structural Members and Buckling
Failure Theories and Energy Methods
Flight Vehicle Structures
Structural Dynamics
Theory of Elasticity

Stress and Strain – Basics and Types

Understanding the behavior of materials under external forces is fundamental to the study of strength of materials. The concepts of stress and strain help us quantify internal forces and deformations in structural members.

1. Introduction

When a force is applied to a body, it tends to deform. The internal resistance offered by the material to this deformation is known as stress, and the deformation per unit dimension is known as strain.

These two quantities form the foundation for analyzing load-carrying components in aircraft structures, mechanical systems, and civil frameworks.

2. Stress

2.1 Definition

Stress is defined as the internal force acting per unit area within a body subjected to external loading.

\sigma = \frac{F}{A}

Where:

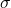  • \sigma = normal stress (in N/m² or Pa)
  • F = internal force acting normal to the surface (in N)
  • A = cross-sectional area over which the force acts (in m²)

2.2 Types of Stress

  • Normal Stress: Acts perpendicular to the surface.
    • Tensile Stress: When the member is being stretched.
    • Compressive Stress: When the member is being shortened or compressed.
  • Shear Stress: Acts tangentially to the surface.

\tau = \frac{V}{A}

Where \tau = shear stress, V = shear force.

  • Bearing Stress: Localized stress at the contact area between two bodies, often encountered in riveted or bolted joints.

3. Strain

3.1 Definition

Strain is the measure of deformation representing the displacement between particles in the material body.

\varepsilon = \frac{\delta}{L}

Where:

  • \varepsilon = normal strain (dimensionless)
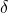  • \delta = change in length
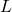  • L = original length

3.2 Types of Strain

  • Normal Strain: Change in length per unit length in the direction of the applied load.
    • Tensile Strain: Elongation
    • Compressive Strain: Contraction
  • Shear Strain (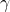\gamma): Angular distortion between two orthogonal planes.

\gamma = \frac{\Delta x}{L}

Where \Delta x is the relative displacement between layers and L is the perpendicular distance between them.

4. Stress-Strain Relationship

In the linear elastic range, stress and strain are proportional:

\sigma = E \varepsilon

Where E is the Young’s modulus or modulus of elasticity.

For shear:

\tau = G \gamma

Where G is the shear modulus.

5. Hooke’s Law

Hooke’s Law governs linear elastic behavior:

“Within the elastic limit of a material, the stress is directly proportional to the strain produced.”

This relationship defines the stiffness of a material and is valid only up to the proportional limit on the stress-strain curve.

6. Volumetric Strain

When stress is applied in multiple directions, the volume of the body may change.

\varepsilon_v = \frac{\Delta V}{V}

Where \varepsilon_v is the volumetric strain.

For small strains in 3D:

\varepsilon_v = \varepsilon_x + \varepsilon_y + \varepsilon_z

7. Poisson’s Ratio

Poisson’s ratio (\nu) describes the negative ratio of lateral to axial strain:

\nu = -\frac{\varepsilon_{\text{lateral}}}{\varepsilon_{\text{axial}}}

Typical values:

  • Aluminum: ~0.33
  • Steel: ~0.30
  • Rubber: ~0.49

8. Conclusion

The concepts of stress and strain form the cornerstone of all structural analysis. They help engineers design safe and efficient structures by predicting how materials will behave under different loading conditions.

In aircraft structures, accurate stress and strain analysis is critical due to the need for lightweight, reliable components operating under extreme conditions.

Shopping Cart
Scroll to Top