
Structures
Principal Stresses and Strains
In structural analysis and design, understanding the internal stress state at a point within a material is essential. Often, the stress components are resolved along an arbitrary coordinate system, but for clarity in design and failure analysis, it’s useful to find the principal stresses and strains—the extreme values of normal stress or strain at a point with no shear component. These help engineers assess critical conditions, such as yielding or fracture.
1. Stress Components at a Point
In a general three-dimensional stress state, the stress at a point is described by the stress tensor:
![]()
Here:
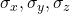 are normal stresses,
are normal stresses,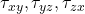 are shear stresses.
are shear stresses.
For simplicity, let us first consider plane stress (2D case), where stress components in the third direction are negligible.
2. Concept of Principal Stresses
Principal stresses are the maximum and minimum normal stresses that occur at particular orientations of the material element, where shear stress is zero. These orientations are known as principal planes.
At these principal planes:
- The stress vector is normal to the plane.
- The shear stress components vanish.
3. Principal Stresses in 2D (Plane Stress Condition)
Let a material be subjected to normal stresses ![]() ,
, ![]() , and a shear stress
, and a shear stress ![]() . The principal stresses
. The principal stresses ![]() and
and ![]() are obtained from:
are obtained from:
![]()
Where:
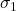 is the major principal stress (maximum),
is the major principal stress (maximum),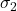 is the minor principal stress (minimum).
is the minor principal stress (minimum).
Orientation of Principal Planes:
The angle ![]() of the principal planes (measured counterclockwise from the x-axis) is given by:
of the principal planes (measured counterclockwise from the x-axis) is given by:
![]()
4. Principal Stresses in 3D
In three-dimensional stress states, there are three principal stresses ![]() which are the eigenvalues of the stress tensor. These are the roots of the characteristic equation:
which are the eigenvalues of the stress tensor. These are the roots of the characteristic equation:
![]()
Expanded as the cubic equation:
![]()
Where ![]() represents a principal stress and:
represents a principal stress and:
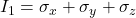 (first invariant),
(first invariant),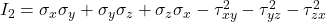 ,
,![Rendered by QuickLaTeX.com I_3 = \det[\sigma_{ij}]](https://gateing.com/wp-content/ql-cache/quicklatex.com-eea533a6b5f39ff36092829aaf17220a_l3.png) (third invariant, the determinant of the stress tensor).
(third invariant, the determinant of the stress tensor).
5. Principal Strains
Similarly, principal strains are the extreme values of normal strain occurring at orientations where shear strain is zero.
For 2D strain state, given:
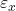 ,
,  : normal strains,
: normal strains, : shear strain (engineering strain),
: shear strain (engineering strain),
The principal strains are given by:
![]()
Angle of orientation:
![]()
6. Graphical Representation: Mohr’s Circle
Mohr’s Circle provides a visual method to determine:
- Principal stresses and strains,
- Maximum shear stress and its orientation.
The radius of Mohr’s circle is equal to the maximum shear stress:
![]()
7. Significance in Aircraft Structures
Aircraft components are subjected to multiaxial stress states. Evaluating principal stresses helps:
- Locate the most critical stress points,
- Apply appropriate failure theories (e.g., von Mises, Tresca),
- Design components for lightweight strength and durability.
Principal stress and strain calculations form the basis for stress checks in fuselage skins, wing spars, and bulkheads.
8. Summary
- Principal stresses/strains are extreme normal stresses/strains with zero shear.
- Their computation simplifies complex stress states and supports safety-critical design.
- They can be found analytically using transformation equations or graphically via Mohr’s circle.
These values are foundational in structural mechanics and essential for applying modern failure criteria in aerospace engineering.
Let me know when you’re ready for the next topic, or if you’d like this rewritten in a shorter or more visual format.

