Insights and Tips for GATE Aspirants

Course Image

Structures

Course Progress: 0% (0/48 topics completed)

⏹️ Course Syllabus
Strength of Materials
Structural Members and Buckling
Failure Theories and Energy Methods
Flight Vehicle Structures
Structural Dynamics
Theory of Elasticity

3D Stress and Strain Transformations

In many structural applications, stresses and strains act in multiple directions simultaneously. For such 3D states, it’s essential to understand how these quantities transform when observed from different orientations — a fundamental requirement for analyzing aircraft structures that undergo complex loading.

1. Stress at a Point in 3D

At any point within a solid, the state of stress is defined by a set of normal and shear stress components acting on three mutually perpendicular planes (x, y, z axes).

The stress tensor in three dimensions is given by:

\left[ \sigma \right] = \begin{bmatrix} \sigma_x & \tau_{xy} & \tau_{xz} \ \tau_{yx} & \sigma_y & \tau_{yz} \ \tau_{zx} & \tau_{zy} & \sigma_z \end{bmatrix}

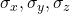  • \sigma_x, \sigma_y, \sigma_z: Normal stresses
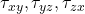  • \tau_{xy}, \tau_{yz}, \tau_{zx}: Shear stresses

For equilibrium and symmetry:

\tau_{xy} = \tau_{yx},\quad \tau_{yz} = \tau_{zy},\quad \tau_{zx} = \tau_{xz}

2. Transformation of Stress

When the coordinate system is rotated, the stress components on the new planes also change. The stress transformation equations allow us to calculate the new stress components along any arbitrary plane passing through a point.

2.1 Stress Transformation Matrix Form

If \hat{n} is a unit vector normal to a plane with direction cosines (l, m, n), the traction vector on that plane is:

\mathbf{T}^{(n)} = \left[ \sigma \right] \cdot \hat{n}

The normal stress on the plane:

\sigma_n = \hat{n} \cdot \mathbf{T}^{(n)}

The shear stress is the component of \mathbf{T}^{(n)} perpendicular to \hat{n}.

2.2 Principal Stresses (3D)

The principal stresses are the eigenvalues of the stress tensor. They satisfy the characteristic equation:

\left| \left[ \sigma \right] - \sigma_p \mathbf{I} \right| = 0

This leads to a cubic equation in \sigma_p:

\sigma_p^3 - I_1 \sigma_p^2 + I_2 \sigma_p - I_3 = 0

Where:

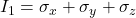  • I_1 = \sigma_x + \sigma_y + \sigma_z (first invariant)

I_2 = \sigma_x \sigma_y + \sigma_y \sigma_z + \sigma_z \sigma_x - \tau_{xy}^2 - \tau_{yz}^2 - \tau_{zx}^2

I_3 = \text{det} \left[ \sigma \right]

Solving this gives the three principal stresses \sigma_1, \sigma_2, \sigma_3.

3. Strain in 3D

Strain in 3D is similarly represented using a strain tensor:

\left[ \varepsilon \right] = \begin{bmatrix} \varepsilon_x & \gamma_{xy}/2 & \gamma_{xz}/2 \ \gamma_{xy}/2 & \varepsilon_y & \gamma_{yz}/2 \ \gamma_{xz}/2 & \gamma_{yz}/2 & \varepsilon_z \end{bmatrix}

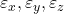  • \varepsilon_x, \varepsilon_y, \varepsilon_z: Normal strains
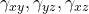  • \gamma_{xy}, \gamma_{yz}, \gamma_{xz}: Engineering shear strains

Note: In tensor form, shear strain is taken as half the engineering strain.

4. Transformation of Strain

Strain transformation follows a process similar to stress transformation. The transformed strain components on an arbitrary plane can be derived using tensor rotation rules.

Principal strains are obtained by solving the eigenvalue problem for the strain tensor.

5. Octahedral Stresses and Strains

These represent average quantities acting on planes equally inclined to the coordinate axes.

5.1 Octahedral Normal Stress:

\sigma_{\text{oct}} = \frac{1}{3}(\sigma_x + \sigma_y + \sigma_z)

5.2 Octahedral Shear Stress:

\tau_{\text{oct}} = \frac{1}{3} \sqrt{ (\sigma_x - \sigma_y)^2 + (\sigma_y - \sigma_z)^2 + (\sigma_z - \sigma_x)^2 + 6(\tau_{xy}^2 + \tau_{yz}^2 + \tau_{zx}^2) }

These are particularly useful in formulating yield criteria like von Mises stress.

6. Application in Aircraft Structures

In aerospace applications, components experience complex multiaxial stress states due to:

  • Combined bending and torsion in wings and fuselages
  • Pressure and thermal loads on thin-walled structures
  • In-plane shear and axial loads on stiffened panels

Hence, accurate 3D stress and strain transformation analysis is critical for safe and efficient design.

7. Summary

  • The state of stress or strain at a point is best described using tensors.
  • Transformation laws allow evaluation of these quantities on rotated planes.
  • Principal stresses/strains are key for failure and deformation predictions.
  • These tools form the backbone of modern structural analysis, especially in thin-walled aerospace structures with multiaxial loading.

Understanding and applying 3D transformation principles ensures engineers can anticipate and manage complex material behavior under real-world loading conditions.

Shopping Cart
Scroll to Top