
Structures
Mohr’s Circle for Stress and Strain
Mohr’s Circle is a powerful graphical tool used to visualize the state of stress or strain at a point and determine important quantities like principal stresses/strains, maximum shear stress/strain, and the orientation of planes on which these act. It is widely used in structural and materials engineering due to its intuitive and elegant geometric interpretation of transformation equations.
1. Purpose of Mohr’s Circle
Mohr’s Circle helps to:
- Find principal stresses and principal planes,
- Find maximum shear stresses and the angles of maximum shear,
- Transform stresses from one coordinate system to another,
- Gain a visual understanding of the relationship between normal and shear stress.
It can be used for both:
- Stress transformation: in 2D plane stress or strain problems,
- Strain transformation: where strains (including shear strains) are represented graphically.
2. Mohr’s Circle for Plane Stress
Consider a plane stress state with:
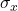 ,
,  : normal stresses in the x and y directions,
: normal stresses in the x and y directions,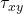 : shear stress.
: shear stress.
Center and Radius of the Circle
- Center of the circle:
![]()
Radius of the circle:
![]()
Principal Stresses
- The coordinates of the points where the circle intersects the horizontal axis (i.e., no shear stress) are the principal stresses:
![]()
Maximum Shear Stress
- The maximum shear stress is the radius of the circle:
![]()
This occurs at a point rotated by ![]() from the principal plane.
from the principal plane.
3. Drawing Mohr’s Circle (Stress)
- Plot the point A =
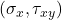
- Plot the point B =

- Find the center C = midpoint of AB
- Draw a circle with radius equal to the distance from C to A or B
- The horizontal intercepts of the circle are
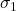 and
and 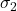
- The vertical intercepts give the maximum shear stress
Important Note: In Mohr’s circle:
- The horizontal axis represents normal stress (
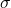 )
) - The vertical axis represents shear stress (
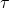 )
) - Clockwise shear is considered negative, and counterclockwise shear is positive (sign convention)
4. Mohr’s Circle for Plane Strain
In strain analysis, similar rules apply, but:
- Engineering shear strain (
 ) is halved in the Mohr’s circle:
) is halved in the Mohr’s circle:
![]()
The principal strains are:
![]()
Center and radius:
![]()
The rest of the construction and interpretation is identical to that of the stress case.
5. Rotation of Axes and Angle Interpretation
- If the element is rotated by angle
 in real space, the angle in Mohr’s Circle is
in real space, the angle in Mohr’s Circle is 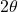 .
. - Principal planes and maximum shear planes are separated by
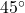 in Mohr’s circle (which corresponds to
in Mohr’s circle (which corresponds to 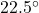 in real space).
in real space).
6. Example Case (Numerical)
Let:
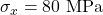 ,
,  ,
, 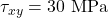
Then,
- Center:
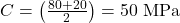
- Radius:
![]()
Principal stresses:
![]()
Maximum shear stress: ![]()
7. Applications in Aerospace Structures
- Mohr’s Circle is used to analyze stresses in thin-walled fuselage skins, bulkheads, stringers, and wing spars.
- It helps identify locations where failure theories (like Tresca or von Mises) should be applied.
- Mohr’s circle provides engineers with a quick method to analyze multiaxial stress conditions, especially in finite element outputs or load cases.
8. Summary
- Mohr’s Circle is a geometric tool to understand stress/strain transformations.
- It simplifies the calculation of principal and shear components.
- It is based on the same equations as transformation formulas, but offers visual clarity.
- For 2D problems, it gives insight into the full range of stress/strain at a point and the safe orientations for loading.

